
【题目】已知不等式组 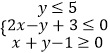 表示的平面区域为D,若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围是( )
表示的平面区域为D,若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围是( )
A.[10,+∞)
B.[11,+∞)
C.[13,+∞)
D.[14,+∞)
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =﹣20,
=﹣20, ![]() =
= ![]() ﹣
﹣ ![]()
![]()
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入﹣成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在三棱锥P﹣ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示. 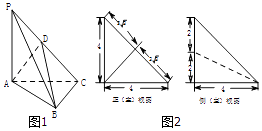
(1)证明:AD⊥BC;
(2)求三棱锥D﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,设命题p:函数y=ax在R上单调递增;命题q:不等式ax2﹣ax+1>0对x∈R恒成立,若p且q为假,p或q为真,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PC⊥平面ABC,∠PAC=30°,∠ACB=45°,BC=2 ![]() ,PA⊥AB.
,PA⊥AB. 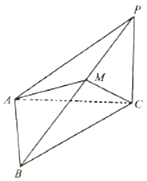
(1)求PC的长;
(2)若点M在侧棱PB上,且 ![]() ,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国古代著名的数学专著《九章算术》里有﹣段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里:驽马初日行九十七里,日减半里,良马先至齐,复还迎驽马,二马相逢, 问:需日相逢.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估.该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入 ![]() 万作为技改费用,投入(50+2x)万元作为宣传费用.试问:当该商品改革后的销售量a至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
万作为技改费用,投入(50+2x)万元作为宣传费用.试问:当该商品改革后的销售量a至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(2x+ ![]() )+
)+ ![]() cos(2x+
cos(2x+ ![]() ),则( )
),则( )
A.y=f(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
B.y=f(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
C.y=f(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
D.y=f(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°、45°,且A、B两点之间的距离为60m,则树的高度为( ) 
A.(30+30 ![]() ) m
) m
B.(30+15 ![]() ) m??
) m??
C.(15+30 ![]() ) m
) m
D.(15+15 ![]() ) m
) m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com