
已知双曲线 的左,右焦点分别为
的左,右焦点分别为 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且 ,则此双曲线的离心率e的最大值为 .
,则此双曲线的离心率e的最大值为 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知椭圆C: +
+ =1(a>b>0),直线l:y=kx+m(k≠0,m≠0),直线l交椭圆C与P,Q两点.
=1(a>b>0),直线l:y=kx+m(k≠0,m≠0),直线l交椭圆C与P,Q两点.
(Ⅰ)若k=1,椭圆C经过点( ,1),直线l经过椭圆C的焦点和顶点,求椭圆方程;
,1),直线l经过椭圆C的焦点和顶点,求椭圆方程;
(Ⅱ)若k= ,b=1,且kOP,k,kOQ成等比数列,求三角形OPQ面积S的取值范围.
,b=1,且kOP,k,kOQ成等比数列,求三角形OPQ面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
在等差数列{an}中,a2=1,a4=5,则{an}的前5项和S5=( )
A.7 B.15 C.20 D.25
查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
函数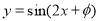 的图象沿x轴向左平移
的图象沿x轴向左平移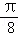 个单位后,得到一个偶函数的图象,则φ的一个可能的值为( ).
个单位后,得到一个偶函数的图象,则φ的一个可能的值为( ).
A. B.
B.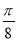 C.
C.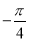 D.
D.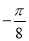
查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥。现有一正三棱锥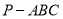 放置在平面
放置在平面 上,已知它的底面边长为2,高为
上,已知它的底面边长为2,高为 ,
, 在平面
在平面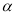 上,现让它绕
上,现让它绕 转动,并使它在某一时刻在平面
转动,并使它在某一时刻在平面 上的射影是等腰直角三角形,则
上的射影是等腰直角三角形,则 的取值范围是( ).
的取值范围是( ).
A. B.
B. C.
C.

 . D.
. D.

查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期期中理科数学试卷(解析版) 题型:选择题
现有四个函数:① ;②
;② ;③
;③ ; ④
; ④ 的图象(部分)如下,但顺序被打乱,则按照从左到右的顺序对应的函数序号是( )
的图象(部分)如下,但顺序被打乱,则按照从左到右的顺序对应的函数序号是( )

A.④①②③ B.①④②③ C.①④③② D.③④②①
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
设 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若 ,则
,则 B.若
B.若 ,则
,则
C.若 ,则
,则 D.若
D.若 ,则
,则
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com