
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥。现有一正三棱锥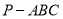 放置在平面
放置在平面 上,已知它的底面边长为2,高为
上,已知它的底面边长为2,高为 ,
, 在平面
在平面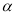 上,现让它绕
上,现让它绕 转动,并使它在某一时刻在平面
转动,并使它在某一时刻在平面 上的射影是等腰直角三角形,则
上的射影是等腰直角三角形,则 的取值范围是( ).
的取值范围是( ).
A. B.
B. C.
C.

 . D.
. D.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试理科数学试卷(解析版) 题型:填空题
已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l:y=x﹣1被该圆所截得的弦长为 ,则圆C的标准方程为 _________ .
,则圆C的标准方程为 _________ .
查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
(本题满分10分)已知数列 的首项
的首项 ,
,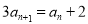 ,
, ,
,
(1)求证:数列 为等比数列;
为等比数列;
(2)若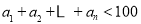 ,求最大的正整数
,求最大的正整数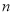 .
.
查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高二下学期期末考试文科数学试卷(解析版) 题型:填空题
已知双曲线 的左,右焦点分别为
的左,右焦点分别为 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且 ,则此双曲线的离心率e的最大值为 .
,则此双曲线的离心率e的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
将函数y=cos2x的图象向右平移 个单位长度,再将所得图象的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的函数解析式为( ).
个单位长度,再将所得图象的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的函数解析式为( ).
A.y=sinx B.y=-cos4x C.y=sin4x D.y=cosx
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期期中理科数学试卷(解析版) 题型:解答题
如图,已知长方形 中,
中, ,
,  ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 .
.
(1)求证: ;
;
(2)若点 是线段
是线段 的中点,求二面角
的中点,求二面角 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二上学期期末考试文科数学试卷(解析版) 题型:解答题
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,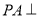 平面
平面 ,
, ,
, ,
, 依次是
依次是 的中点.
的中点.

(1)求证: ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com