
若椭圆![]() =1(m>n>0)和双曲线
=1(m>n>0)和双曲线![]() =1(a>0,b>0)有相同的焦点F1和F2,点P是两曲线的一个交点(如图所示).
=1(a>0,b>0)有相同的焦点F1和F2,点P是两曲线的一个交点(如图所示).
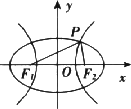
求证:(1)|PF1|·|PF2|=m2-a2;
(2)△PF1F2的面积S=nb.
科目:高中数学 来源:中学教材标准学案 数学 高二上册 题型:013
若椭圆![]() +
+![]() =1(m>n>0)与双曲线
=1(m>n>0)与双曲线![]() -
-![]() =1(a>0,b>0)有相同的焦点F1、F2,点P是它们的交点,则|PF1|·|PF2|的值为
=1(a>0,b>0)有相同的焦点F1、F2,点P是它们的交点,则|PF1|·|PF2|的值为
[ ]
查看答案和解析>>
科目:高中数学 来源:高三数学教学与测试 题型:013
若椭圆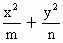 =1(m>n>0)和双曲线
=1(m>n>0)和双曲线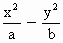 =1(a>0,b>0)有相同的焦点
=1(a>0,b>0)有相同的焦点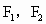 ,P是两条曲线的一个交点,则
,P是两条曲线的一个交点,则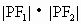 的值为
的值为
[ ]
A.m-a
B.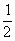 (m-a)
(m-a)
C.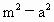 D.
D.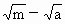
查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-2-1苏教版 苏教版 题型:013
若椭圆![]() =1(m>n>0)和双曲线
=1(m>n>0)和双曲线![]() =1(a>b>0)有相同的左、右焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是
=1(a>b>0)有相同的左、右焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是
m-a
![]() (m-a)
(m-a)
m2-a2
![]()
查看答案和解析>>
科目:高中数学 来源:河南省郑州市智林学校2011届高三第一次月考理科数学试题 题型:044
已知椭圆E:![]() =1(a>b>0)的左、右焦点分别为F1,F2,点P是x轴上方椭圆E上的一点,且PF1⊥F1F2,|PF1|=
=1(a>b>0)的左、右焦点分别为F1,F2,点P是x轴上方椭圆E上的一点,且PF1⊥F1F2,|PF1|=![]() ,|PF2|=
,|PF2|=![]() .
.
(Ⅰ)求椭圆E的方程和P点的坐标;
(Ⅱ)判断以PF2为直径的圆与以椭圆E的长轴为直径的圆的位置关系;
(Ⅲ)若点G是椭圆C:![]() =1(m>n>0)上的任意一点,F是椭圆C的一个焦点,探究以GF为直径的圆与以椭圆C的长轴为直径的圆的位置关系
=1(m>n>0)上的任意一点,F是椭圆C的一个焦点,探究以GF为直径的圆与以椭圆C的长轴为直径的圆的位置关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com