
°æƒø°øΩÃ≤ƒ‘¯”–ΩÈ…‹£∫‘≤![]() …œµƒµ„
…œµƒµ„![]() ¥¶µƒ«–œfl∑Ω≥ÃŒ™
¥¶µƒ«–œfl∑Ω≥ÃŒ™![]() .Œ“√«Ω´∆‰Ω·¬€Õ∆π„£∫Õ÷‘≤
.Œ“√«Ω´∆‰Ω·¬€Õ∆π„£∫Õ÷‘≤![]() £®
£®![]() £©…œµƒµ„
£©…œµƒµ„![]() ¥¶µƒ«–œfl∑Ω≥ÃŒ™
¥¶µƒ«–œfl∑Ω≥ÃŒ™![]() £¨‘⁄Ω‚±æ ±ø…“‘÷±Ω””¶”√.“—÷™£¨÷±œfl
£¨‘⁄Ω‚±æ ±ø…“‘÷±Ω””¶”√.“—÷™£¨÷±œfl![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() £∫
£∫![]() £®
£®![]() £©”–«“÷ª”–“ª∏ˆπ´π≤µ„.
£©”–«“÷ª”–“ª∏ˆπ´π≤µ„.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©…Ë![]() Œ™◊¯±Í‘≠µ„£¨π˝Õ÷‘≤
Œ™◊¯±Í‘≠µ„£¨π˝Õ÷‘≤![]() …œµƒ¡Ωµ„
…œµƒ¡Ωµ„![]() °¢
°¢![]() ∑÷±◊˜∏√Õ÷‘≤µƒ¡ΩÃı«–œfl
∑÷±◊˜∏√Õ÷‘≤µƒ¡ΩÃı«–œfl![]() °¢
°¢![]() £¨«“
£¨«“![]() ”Î
”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() .µ±
.µ±![]() ±‰ªØ ±£¨«Û
±‰ªØ ±£¨«Û![]() √ʪ˝µƒ◊Ó¥Û÷µ£ª
√ʪ˝µƒ◊Ó¥Û÷µ£ª
£®3£©»Ù![]() «Õ÷‘≤
«Õ÷‘≤![]()
![]() …œ≤ªÕ¨µƒ¡Ωµ„£¨
…œ≤ªÕ¨µƒ¡Ωµ„£¨![]()
![]() ÷·£¨‘≤
÷·£¨‘≤![]() π˝
π˝![]() «“Õ÷‘≤
«“Õ÷‘≤![]() …œ»Œ“‚“ªµ„∂º≤ª‘⁄‘≤
…œ»Œ“‚“ªµ„∂º≤ª‘⁄‘≤![]() ƒ⁄£¨‘Ú≥∆‘≤
ƒ⁄£¨‘Ú≥∆‘≤![]() Œ™∏√Õ÷‘≤µƒ“ª∏ˆƒ⁄«–‘≤. ‘Œ £∫Õ÷‘≤
Œ™∏√Õ÷‘≤µƒ“ª∏ˆƒ⁄«–‘≤. ‘Œ £∫Õ÷‘≤![]() «∑ҥʑ⁄π˝◊ÛΩπµ„
«∑ҥʑ⁄π˝◊ÛΩπµ„![]() µƒƒ⁄«–‘≤£ø»Ù¥Ê‘⁄£¨«Û≥ˆ‘≤–ƒ
µƒƒ⁄«–‘≤£ø»Ù¥Ê‘⁄£¨«Û≥ˆ‘≤–ƒ![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() £ª£®3£©¥Ê‘⁄£¨
£ª£®3£©¥Ê‘⁄£¨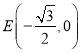
°æΩ‚Œˆ°ø
£®1£©Ω´÷±œfl![]() ¥˙»ÎÕ÷‘≤∑Ω≥㨵√µΩ
¥˙»ÎÕ÷‘≤∑Ω≥㨵√µΩ![]() µƒ∑Ω≥㨔…÷±œfl∫ÕÕ÷‘≤œ‡«–µƒÃıº˛£∫≈–± ΩŒ™0£¨Ω‚∑Ω≥Ãø…µ√
µƒ∑Ω≥㨔…÷±œfl∫ÕÕ÷‘≤œ‡«–µƒÃıº˛£∫≈–± ΩŒ™0£¨Ω‚∑Ω≥Ãø…µ√![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©…Ë«–µ„![]() £¨ø…µ√«–œfl
£¨ø…µ√«–œfl![]() £¨‘Ÿ”…
£¨‘Ÿ”…![]() ¥˙»Î…œ Ω£¨Ω·∫œ¡Ωµ„»∑∂®“ªÃı÷±œfl£¨ø…µ√«–µ„œ“∑Ω≥㨺¥”–
¥˙»Î…œ Ω£¨Ω·∫œ¡Ωµ„»∑∂®“ªÃı÷±œfl£¨ø…µ√«–µ„œ“∑Ω≥㨺¥”–![]() µƒ–±¬ £¨Ω·∫œ¡Ωµ„µƒ–±¬ π´ Ω£¨”…¢Ÿø…µ√
µƒ–±¬ £¨Ω·∫œ¡Ωµ„µƒ–±¬ π´ Ω£¨”…¢Ÿø…µ√![]() µƒ∑Ω≥ÃŒ™
µƒ∑Ω≥ÃŒ™![]() £¨‘À”√µ„µΩ÷±œflµƒæ‡¿Îπ´ Ω∫Õ÷±œfl”ÎÕ÷‘≤∑Ω≥ᙡ¢£¨‘À”√Œ§¥Ô∂®¿Ì∫Õœ“≥§π´ Ω£¨«Ûµ√
£¨‘À”√µ„µΩ÷±œflµƒæ‡¿Îπ´ Ω∫Õ÷±œfl”ÎÕ÷‘≤∑Ω≥ᙡ¢£¨‘À”√Œ§¥Ô∂®¿Ì∫Õœ“≥§π´ Ω£¨«Ûµ√![]() µƒ√ʪ˝£¨ªØºÚ’˚¿Ì£¨‘À”√ª˘±æ≤ªµ» Ωº¥ø…µ√µΩÀ˘«Û◊Ó¥Û÷µ£ª
µƒ√ʪ˝£¨ªØºÚ’˚¿Ì£¨‘À”√ª˘±æ≤ªµ» Ωº¥ø…µ√µΩÀ˘«Û◊Ó¥Û÷µ£ª
£®3£©“¿Ã‚“‚ø…µ√∑˚∫œ“™«Ûµƒ‘≤![]() £¨º¥Œ™π˝µ„
£¨º¥Œ™π˝µ„![]() µƒ»˝Ω«–ŒµƒÕ‚Ω”‘≤.À˘“‘‘≤–ƒ‘⁄
µƒ»˝Ω«–ŒµƒÕ‚Ω”‘≤.À˘“‘‘≤–ƒ‘⁄![]() ÷·…œ.∏˘æ›Ã‚“‚–¥≥ˆ‘≤
÷·…œ.∏˘æ›Ã‚“‚–¥≥ˆ‘≤![]() µƒ∑Ω≥Ã.”…”⁄‘≤µƒ¥Ê‘⁄±ÿ–Γ™∑˚∫œ£¨Õ÷‘≤…œµƒµ„µΩ‘≤
µƒ∑Ω≥Ã.”…”⁄‘≤µƒ¥Ê‘⁄±ÿ–Γ™∑˚∫œ£¨Õ÷‘≤…œµƒµ„µΩ‘≤![]() 懿εƒ◊Ó–°÷µ «
懿εƒ◊Ó–°÷µ «![]() £¨Ω·∫œÕº–Œø…µ√‘≤–ƒ
£¨Ω·∫œÕº–Œø…µ√‘≤–ƒ![]() ‘⁄œfl∂Œ
‘⁄œfl∂Œ![]() …œ£¨∞Îæ∂◊Ó–°.”÷”…”⁄µ„
…œ£¨∞Îæ∂◊Ó–°.”÷”…”⁄µ„![]() “—÷™£¨º¥ø…«Ûµ√Ω·¬€.
“—÷™£¨º¥ø…«Ûµ√Ω·¬€.
Ω‚£∫£®1£©Ω´÷±œfl![]() ¥˙»ÎÕ÷‘≤∑Ω≥Ã
¥˙»ÎÕ÷‘≤∑Ω≥Ã![]() £¨
£¨
ø…µ√![]() £¨
£¨
”…÷±œfl∫ÕÕ÷‘≤œ‡«–£¨ø…µ√![]() £¨
£¨
Ω‚µ√![]() £®”…
£®”…![]() £©£¨
£©£¨
º¥”–Õ÷‘≤![]() µƒ∑Ω≥ÃŒ™
µƒ∑Ω≥ÃŒ™![]() £ª
£ª
£®2£©…Ë«–µ„![]() £¨
£¨
ø…µ√«–œfl![]() £¨
£¨
”…![]() ”Î
”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨ø…µ√
£¨ø…µ√![]() £¨
£¨
”…¡Ωµ„»∑∂®“ªÃı÷±œfl£¨ø…µ√![]() µƒ∑Ω≥ÃŒ™
µƒ∑Ω≥ÃŒ™![]() £¨
£¨
º¥Œ™![]() £¨
£¨
‘≠µ„µΩ÷±œfl![]() µƒæ‡¿ÎŒ™
µƒæ‡¿ÎŒ™![]() £¨
£¨
”…![]() œ˚»•
œ˚»•![]() £¨ø…µ√
£¨ø…µ√![]() £¨
£¨![]() £¨
£¨
ø…µ√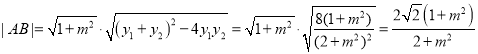 £¨
£¨
ø…µ√![]() µƒ√ʪ˝
µƒ√ʪ˝![]() £¨
£¨
…Ë![]() £¨
£¨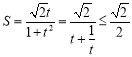 £¨
£¨
µ±«“Ωˆµ±![]() º¥
º¥![]() ±£¨
±£¨![]() »°µ√◊Ó¥Û÷µ
»°µ√◊Ó¥Û÷µ![]() £ª
£ª
£®3£©Õ÷‘≤µƒ∂‘≥∆–‘£¨ø…“‘…Ë![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() ÷·…œ£¨…˵„
÷·…œ£¨…˵„![]() £¨
£¨
‘Ú‘≤![]() µƒ∑Ω≥ÃŒ™£∫
µƒ∑Ω≥ÃŒ™£∫![]() £¨
£¨
”…ƒ⁄«–‘≤∂®“Â÷™µ¿£¨Õ÷‘≤…œµƒµ„µΩµ„![]() 懿εƒ◊Ó–°÷µ «
懿εƒ◊Ó–°÷µ «![]() £¨
£¨
…˵„![]() «Õ÷‘≤
«Õ÷‘≤![]() …œ»Œ“‚“ªµ„£¨
…œ»Œ“‚“ªµ„£¨
‘Ú![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() ◊Ó–°£¨
◊Ó–°£¨![]() £¨¢Ÿ£¨
£¨¢Ÿ£¨
”÷‘≤![]() π˝µ„
π˝µ„![]() £¨
£¨![]() £¨¢⁄
£¨¢⁄
µ„![]() ‘⁄Õ÷‘≤…œ£¨
‘⁄Õ÷‘≤…œ£¨![]() £¨¢€
£¨¢€
”…¢Ÿ¢⁄¢€£¨Ω‚µ√£∫![]() ªÚ
ªÚ![]() £¨
£¨
”÷![]() ±£¨
±£¨![]() £¨≤ª∫œÃ‚“‚£¨
£¨≤ª∫œÃ‚“‚£¨
◊€…œ£∫Õ÷‘≤![]() ¥Ê‘⁄∑˚∫œÃıº˛µƒƒ⁄«–‘≤£¨µ„
¥Ê‘⁄∑˚∫œÃıº˛µƒƒ⁄«–‘≤£¨µ„![]() µƒ◊¯±Í «
µƒ◊¯±Í «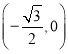 .
.



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë∫Ø ˝![]() £¨∆‰÷–
£¨∆‰÷–![]() £¨
£¨![]() «◊‘»ª∂‘ ˝µƒµ◊ ˝.
«◊‘»ª∂‘ ˝µƒµ◊ ˝.
£®1£©»Ù![]() ‘⁄
‘⁄![]() …œ¥Ê‘⁄¡Ω∏ˆº´÷µµ„£¨«Û
…œ¥Ê‘⁄¡Ω∏ˆº´÷µµ„£¨«Û![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®2£©»Ù![]() £¨÷§√˜£∫
£¨÷§√˜£∫![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™F «≈◊ŒÔœflC£∫![]() µƒΩ𵄣¨π˝E(©Ål£¨0)µƒ÷±œfl
µƒΩ𵄣¨π˝E(©Ål£¨0)µƒ÷±œfl![]() ”Î≈◊ŒÔœfl∑÷ÑeΩª”⁄A£¨B¡Ωµ„£®µ„A£¨B‘⁄x÷·µƒ…œ∑Ω£©£Æ
”Î≈◊ŒÔœfl∑÷ÑeΩª”⁄A£¨B¡Ωµ„£®µ„A£¨B‘⁄x÷·µƒ…œ∑Ω£©£Æ
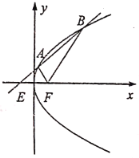
£®1£©…Ë÷±œflAF£¨BFµƒ–±¬ ∑÷ÑeŒ™![]() £¨
£¨![]() £¨÷§√˜£∫
£¨÷§√˜£∫![]() £ª
£ª
£®2£©»Ù![]() ABFµƒ√ʪ˝Œ™4£¨«Û÷±œfl
ABFµƒ√ʪ˝Œ™4£¨«Û÷±œfl![]() µƒ∑Ω≥ãÆ
µƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„![]() «À´«˙œfl
«À´«˙œfl![]()
![]() …œµƒ∂ص„£¨
…œµƒ∂ص„£¨![]() «À´«˙œflµƒΩ𵄣¨M «
«À´«˙œflµƒΩ𵄣¨M «![]() µƒ∆Ω∑÷œfl…œ“ªµ„£¨«“
µƒ∆Ω∑÷œfl…œ“ªµ„£¨«“![]() £¨ƒ≥Õ¨—ß”√“‘œ¬∑Ω∑®—–æø
£¨ƒ≥Õ¨—ß”√“‘œ¬∑Ω∑®—–æø![]() £∫—”≥§
£∫—”≥§![]() Ωª
Ωª![]() ”⁄µ„N£¨ø…÷™
”⁄µ„N£¨ø…÷™![]() Œ™µ»—¸»˝Ω«–Œ£¨«“MŒ™
Œ™µ»—¸»˝Ω«–Œ£¨«“MŒ™![]() µƒ÷–µ„£¨µ√
µƒ÷–µ„£¨µ√![]() £¨¿‡À∆µÿ£∫µ„
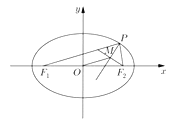
£¨¿‡À∆µÿ£∫µ„![]() «Õ÷‘≤
«Õ÷‘≤![]()
![]() …œµƒ∂ص„£¨
…œµƒ∂ص„£¨![]() Õ÷‘≤µƒΩ𵄣¨M «
Õ÷‘≤µƒΩ𵄣¨M «![]() µƒ∆Ω∑÷œfl…œ“ªµ„£¨«“
µƒ∆Ω∑÷œfl…œ“ªµ„£¨«“![]() ‘Ú
‘Ú![]() µƒ»°÷µ∑∂Œß «______
µƒ»°÷µ∑∂Œß «______

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
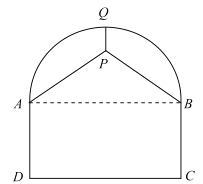
°æƒø°ø»ÁÕº£¨ƒ≥À̵¿µƒ∆ √ÊÕº «”…∞Α≤º∞æÿ–Œ![]() ◊È≥…£¨ΩªÕ®≤ø√≈ƒ‚‘⁄À̵¿∂•≤ø∞≤◊∞Õ®∑Á…˱∏£® ”◊˜µ„
◊È≥…£¨ΩªÕ®≤ø√≈ƒ‚‘⁄À̵¿∂•≤ø∞≤◊∞Õ®∑Á…˱∏£® ”◊˜µ„![]() £©£¨Œ™¡ÀπÃ∂®∏√…˱∏£¨º∆ªÆ≥˝¥”À̵¿◊Ó∏flµ„
£©£¨Œ™¡ÀπÃ∂®∏√…˱∏£¨º∆ªÆ≥˝¥”À̵¿◊Ó∏flµ„![]() ¥¶ π”√∏÷π‹¥π÷±œÚœ¬µı◊∞“‘Õ‚£¨‘Ÿ‘⁄¡Ω≤‡◊‘
¥¶ π”√∏÷π‹¥π÷±œÚœ¬µı◊∞“‘Õ‚£¨‘Ÿ‘⁄¡Ω≤‡◊‘![]() ¡Ωµ„∑÷± π”√∏÷π‹÷ß≥≈.“—÷™µ¿¬∑øÌ
¡Ωµ„∑÷± π”√∏÷π‹÷ß≥≈.“—÷™µ¿¬∑øÌ![]() £¨…˱∏“™«Û∞≤◊∞‘⁄∞Α≤ƒ⁄≤ø£¨À˘ π”√µƒ∏÷π‹◊‹≥§∂»Œ™
£¨…˱∏“™«Û∞≤◊∞‘⁄∞Α≤ƒ⁄≤ø£¨À˘ π”√µƒ∏÷π‹◊‹≥§∂»Œ™![]() .
.
£®1£©¢Ÿ…Ë![]() £¨Ω´
£¨Ω´![]() ±Ì 挙πÿ”⁄
±Ì 挙πÿ”⁄![]() µƒ∫Ø ˝£ª
µƒ∫Ø ˝£ª
¢⁄…Ë![]() £¨Ω´
£¨Ω´![]() ±Ì 挙πÿ”⁄
±Ì 挙πÿ”⁄![]() µƒ∫Ø ˝£ª
µƒ∫Ø ˝£ª
£®2£©«Î—°”√£®1£©÷–µƒ“ª∏ˆ∫Ø ˝πÿœµ Ω£¨Àµ√˜»Á∫Œ…˺∆£¨À˘”√µƒ∏÷π‹≤ƒ¡œ◊Ó °£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ◊Û”“Ωπµ„∑÷±Œ™
µƒ◊Û”“Ωπµ„∑÷±Œ™![]() £¨¿Î–ƒ¬ Œ™
£¨¿Î–ƒ¬ Œ™![]() £¨
£¨![]() «Õ÷‘≤
«Õ÷‘≤![]() …œµƒ“ª∏ˆ∂ص„£¨«“
…œµƒ“ª∏ˆ∂ص„£¨«“![]() √ʪ˝µƒ◊Ó¥Û÷µŒ™
√ʪ˝µƒ◊Ó¥Û÷µŒ™![]() .
.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©…Ë÷±œfl![]() –±¬ Œ™
–±¬ Œ™![]() £¨«“
£¨«“![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() µƒ¡Ì“ª∏ˆΩªµ„Œ™
µƒ¡Ì“ª∏ˆΩªµ„Œ™![]() £¨ «∑ҥʑ⁄µ„
£¨ «∑ҥʑ⁄µ„![]() £¨ πµ√
£¨ πµ√![]() »Ù¥Ê‘⁄£¨«Û
»Ù¥Ê‘⁄£¨«Û![]() µƒ»°÷µ∑∂Œß£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
µƒ»°÷µ∑∂Œß£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“π˙ « ¿ΩÁ…œ—œ÷ÿ»±ÀƵƒπ˙º“£¨ƒ≥ –’˛∏ÆŒ™¡Àπƒ¿¯æ”√ÒΩ⁄‘º”√ÀÆ£¨º∆ªÆµ˜’˚æ”√Ò…˙ªÓ”√ÀÆ ’∑—∑Ω∞∏£¨ƒ‚»∑∂®“ª∏ˆ∫œ¿Ìµƒ‘¬”√ÀÆ¡ø±Í◊º![]() £®∂÷£©°¢“ªŒªæ”√Òµƒ‘¬”√ÀÆ¡ø≤ª≥¨π˝
£®∂÷£©°¢“ªŒªæ”√Òµƒ‘¬”√ÀÆ¡ø≤ª≥¨π˝![]() µƒ≤ø∑÷∞¥∆Ωº€ ’∑—£¨≥¨≥ˆ
µƒ≤ø∑÷∞¥∆Ωº€ ’∑—£¨≥¨≥ˆ![]() µƒ≤ø∑÷∞¥“Ⱥ€ ’∑—.Œ™¡À¡ÀΩ‚æ”√Ò”√ÀÆ«Èøˆ£¨Õ®π˝≥È—˘£¨ªÒµ√¡Àƒ≥ƒÍ100Œªæ”√Ò√ø»Àµƒ‘¬æ˘”√ÀÆ¡ø£®µ•Œª£∫∂÷£©£¨Ω´ ˝æ›∞¥’’[0,0.5)£¨[0.5,1)£¨°≠£¨[4,4.5]∑÷≥…9◊È£¨÷∆≥…¡À»ÁÕºÀ˘ 浃∆µ¬ ∑÷≤º÷±∑ΩÕº.
µƒ≤ø∑÷∞¥“Ⱥ€ ’∑—.Œ™¡À¡ÀΩ‚æ”√Ò”√ÀÆ«Èøˆ£¨Õ®π˝≥È—˘£¨ªÒµ√¡Àƒ≥ƒÍ100Œªæ”√Ò√ø»Àµƒ‘¬æ˘”√ÀÆ¡ø£®µ•Œª£∫∂÷£©£¨Ω´ ˝æ›∞¥’’[0,0.5)£¨[0.5,1)£¨°≠£¨[4,4.5]∑÷≥…9◊È£¨÷∆≥…¡À»ÁÕºÀ˘ 浃∆µ¬ ∑÷≤º÷±∑ΩÕº.

£®¢Ò£©«Û÷±∑ΩÕº÷–aµƒ÷µ£ª
£®¢Ú£©…Ë∏√ –”–30ÕÚæ”√Ò£¨π¿º∆»´ –æ”√Ò÷–‘¬æ˘”√ÀÆ¡ø≤ªµÕ”⁄3∂÷µƒ»À ˝£¨≤¢Àµ√˜¿Ì”…£ª
£®¢Û£©»Ù∏√ –’˛∏Æœ£Õ˚ π85%µƒæ”√Ò√ø‘¬µƒ”√ÀÆ¡ø≤ª≥¨π˝±Í◊º![]() £®∂÷£©£¨π¿º∆
£®∂÷£©£¨π¿º∆![]() µƒ÷µ£¨≤¢Àµ√˜¿Ì”….
µƒ÷µ£¨≤¢Àµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
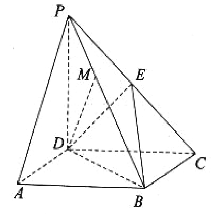
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂![]() ÷–£¨µ◊√Ê
÷–£¨µ◊√Ê![]() «∆Ω––Àƒ±fl–Œ£¨
«∆Ω––Àƒ±fl–Œ£¨![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() «¿‚
«¿‚![]() …œµƒ“ªµ„.
…œµƒ“ªµ„.
£®1£©»Ù![]() ∆Ω√Ê
∆Ω√Ê![]() £¨÷§√˜£∫
£¨÷§√˜£∫![]() £ª
£ª
£®2£©‘⁄£®1£©µƒÃıº˛œ¬£¨¿‚![]() …œ «∑ҥʑ⁄µ„
…œ «∑ҥʑ⁄µ„![]() £¨ π÷±œfl
£¨ π÷±œfl![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…Ω«µƒ¥Û–°Œ™
À˘≥…Ω«µƒ¥Û–°Œ™![]() £ø»Ù¥Ê‘⁄£¨«Û
£ø»Ù¥Ê‘⁄£¨«Û![]() µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™œ¬¡–√¸Ã‚£∫
¢Ÿ‘⁄œfl–‘ªÿπȃ£–Õ÷–£¨œ‡πÿ÷∏ ˝![]() ‘ΩΩ”Ω¸”⁄1£¨±Ì æªÿπÈ–ßπ˚‘Ω∫√£ª
‘ΩΩ”Ω¸”⁄1£¨±Ì æªÿπÈ–ßπ˚‘Ω∫√£ª
¢⁄¡Ω∏ˆ±‰¡øœ‡πÿ–‘‘Ω«ø£¨‘Úœ‡πÿœµ ˝ræÕ‘ΩΩ”Ω¸”⁄1£ª
¢€‘⁄ªÿπÈ÷±œfl∑Ω≥Ã![]() ÷–£¨µ±Ω‚ Õ±‰¡ø
÷–£¨µ±Ω‚ Õ±‰¡ø![]() √ø‘ˆº”“ª∏ˆµ•Œª ±£¨‘§±®±‰¡ø
√ø‘ˆº”“ª∏ˆµ•Œª ±£¨‘§±®±‰¡ø![]() ∆Ωæ˘ºı…Ÿ0.5∏ˆµ•Œª£ª
∆Ωæ˘ºı…Ÿ0.5∏ˆµ•Œª£ª
¢‹¡Ω∏ˆƒ£–Õ÷–≤–≤Ó∆Ω∑Ω∫Õ‘Ω–°µƒƒ£–Õƒ‚∫œµƒ–ßπ˚‘Ω∫√.
¢›ªÿπÈ÷±œfl![]() ∫„π˝—˘±æµ„µƒ÷––ƒ
∫„π˝—˘±æµ„µƒ÷––ƒ![]() £¨«“÷¡…Ÿπ˝“ª∏ˆ—˘±æµ„£ª
£¨«“÷¡…Ÿπ˝“ª∏ˆ—˘±æµ„£ª
¢fi»Ù![]() µƒπ€≤‚÷µ¬˙◊„
µƒπ€≤‚÷µ¬˙◊„![]() °›6.635£¨Œ“√«”–99%µƒ∞—Œ’»œŒ™Œ¸—ÔΪº∑Œ≤°”–πÿœµ£¨ƒ«√¥‘⁄100∏ˆŒ¸—õƒ»À÷–±ÿ”–99»Àªº”–∑Œ≤°£ª
°›6.635£¨Œ“√«”–99%µƒ∞—Œ’»œŒ™Œ¸—ÔΪº∑Œ≤°”–πÿœµ£¨ƒ«√¥‘⁄100∏ˆŒ¸—õƒ»À÷–±ÿ”–99»Àªº”–∑Œ≤°£ª
¢fl¥”Õ≥º∆¡ø÷–µ√÷™”–95%µƒ∞—Œ’»œŒ™Œ¸—ÔΪº∑Œ≤°”–πÿœµ£¨ «÷∏”–5%µƒø…ƒ‹–‘ πµ√Õ∆∂œ≥ˆœ÷¥ÌŒÛ£Æ ∆‰÷–’˝»∑√¸Ã‚µƒ–Ú∫≈ «__________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com