运行下列程序:
“INPUT a
i=1
DO
a=2*a-1
i=i+1
LOOP UNTIL i>10
PRNIT a|END”;
若a的输入值来自前十个正整数,则a的输出值属于{1,1025,2252,3049}的概率为________.
0.2
分析:由题设条件中的程序知,此程序中的循环体要运行十次,故a=2*a-1被执行了十次,可由此规律得出输入的数a经过十次运算后的表达式,再由数列的求和公式化简,探讨a的输出值属于{1,1025,2252,3049}个数,即可得到事件“a的输出值属于{1,1025,2252,3049}”包含的基本事件数,而总的基本事件数是10,由公式求出概率
解答:此程序中的循环体要运行十次,故a=2*a-1被执行了十次,
故输入的数a经过十次运算后的表达式为a×210-1×29-1×28-1×27-1×26-1×25-1×24-1×23-1×22-1×21-1=a×210-1×210+1=(a-1)×210+1
当a=1时,输出的结果是1
当a=2时,输出的结果是1025
当a=3时,输出的结果是2049
当a=4时,输出的结果是3072
由上验证知只有当a的值为1,2时,所输出的结果是属于{1,1025,2252,3049}的
又知输入前十个正整数输出的不同值有十个,故事件“a的输出值属于{1,1025,2252,3049}”的概率是0.2
故答案为0.2
点评:本题考查数列的应用,古典概率模型以及算法语句,解题的关键是看懂伪代码,且能从其给出的运算中抽象出等比数列来,从运算过程中抽象出数列模型是解本题的难点,本题综合性强,涉及的考点多,转化时要严谨



 口算题天天练系列答案
口算题天天练系列答案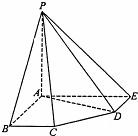 在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE= a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°. 是否存在最值的问题”,你认为以下四种说法中正确的是
是否存在最值的问题”,你认为以下四种说法中正确的是