Question

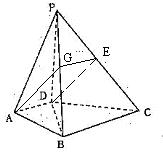
（08年天津南开区质检一理）  （12分） 已知如图，在四棱锥P―ABCD中，PD⊥平面ABCD，AD⊥DC，AD//BC，PD：DC：BC=。

（1）证明BC⊥平面PDC；

（2）求二面角D―PB―C的正切值；

（3）若，求证：平面PAB⊥平面PBC。

Answer 1

解析：本小题考查直线与直线垂直、直线与平面垂直、平面与平面垂直、二面角等基础知识，考查空间想象能力、运算能力和推理论证能力。

（1）解：由PD⊥平面ABCD，平面ABCD，得PD⊥BC

由AD⊥DC，AD//BC，得BC⊥DC

又，则BC⊥平面PDC（3分）

（2）解：取PC中点E，连DE，则DE⊥PC

由BC⊥平面PDC，平面PBC

得平面PDC⊥平面PBC  ∴ DE⊥平面PBC

作EF⊥PB于F，连DF

由三垂线定理，得DF⊥PB

则∠DFE为二面角D―PB―C的平面角

在中，求得

在中，求得

在中，

即二面角D―PB―C的正切值为（8分）

（3）证：取PB中点G，连AG和EG

由三角形中位线定理得GE//BC，

由已知，AD//BC，

∴ AD=GE，AD//GE

则四边形AGED为平行四边形

∴ AG//DE

由（2）已证出DE⊥平面PBC

∴ AG⊥平面PBC

又平面PAB    ∴ 平面PAB⊥平面PBC（12分）