
(本小题满分12分)某单位组织4个部门的职工旅游,规定每个部门只能在韶山、 衡山、张家界3个景区中任选一个,假设各部门选择每个景区是等可能的.
衡山、张家界3个景区中任选一个,假设各部门选择每个景区是等可能的.
(1)是 3个景区都有部门选择的概率是 ;
(2)求恰有2个景区有部门选择的概率
解:某单位的4个部门选择3个景区可能出现的结果数为34.由于是任意选择,这些结
果出现的可能性都相等. …………………………………2分
(1)3个景区都有部门选择可能出现的结果数为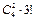 (从4个部门中任选2个作为1组,另外2个部门各作为1组,共3组,共有
(从4个部门中任选2个作为1组,另外2个部门各作为1组,共3组,共有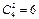 种分法,每组选择不同的景区,共有3!种选法),记“3个景区都有部门选择”为事件A1,那么事件A1的概率为 P(A1)=
种分法,每组选择不同的景区,共有3!种选法),记“3个景区都有部门选择”为事件A1,那么事件A1的概率为 P(A1)=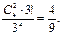 …………………………………7分
…………………………………7分
(2)解法1:分别记“恰有2个景区有部门选择”和“4个部门都选择同一个景区”为事件A2和A3,则事件A3的概率为P(A3)=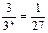 ,事件A2的概率为 P(A2)=1-P(A1)-P(A3)=
,事件A2的概率为 P(A2)=1-P(A1)-P(A3)=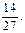 ………………………………12分
………………………………12分
解法2:恰有2个景区有部门选择的结果为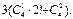 (先从3个景区任意选定2个,共有
(先从3个景区任意选定2个,共有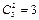 种选法,再让4个部门来选择这2个景区,分两种情况:第一种情况,从4个部门中任取1个作为1组,另外3个部门作为1组,共2组,每组选择2个不同的景区,共有
种选法,再让4个部门来选择这2个景区,分两种情况:第一种情况,从4个部门中任取1个作为1组,另外3个部门作为1组,共2组,每组选择2个不同的景区,共有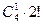 种不同选法.第二种情况,从4个部门中任选2个部门到1个景区,另外2个部门在另1个景区,共有
种不同选法.第二种情况,从4个部门中任选2个部门到1个景区,另外2个部门在另1个景区,共有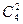 种不同选法).所以
种不同选法).所以
P(A2)=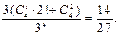 ………………………………12分
………………………………12分
解析


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段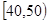 ,
,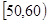 …
…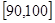 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是40~50分及90~100分的学生中选两人,记他们的成绩为x,y,求满足“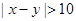 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
两个人射击,甲射击一次中靶概率是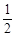 ,乙射击一次中靶概率是
,乙射击一次中靶概率是 ,
,
(Ⅰ)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(Ⅱ)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(Ⅲ)两人各射击5次,是否有99%的把握断定他们至少中靶一次?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(1)若 一次从中随机抽取3张
一次从中随机抽取3张 卡片,求3张卡片上数字之和大于或等于7的概率;
卡片,求3张卡片上数字之和大于或等于7的概率;
(2)若第一次随机抽1张卡片,放回后再随机抽取 1张卡片,求两次抽取中至少一次抽到数字2的概率.
1张卡片,求两次抽取中至少一次抽到数字2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
(1)求n的值;
(2)若高一全体学生平均每天晚自习自主支配学习时间少于45分钟,则学校需要减少作业量.根据以上抽样调查数据,学校是否需要减少作业量?
(注:统计方法中,同一组数据常用该组区间的中点值作为代表)
(3)问卷调查完成后,学校从第3组和第4组学生中利用分层抽样的方法抽取7名学生进行座谈,了解各学科的作业布置情况,并从这7人中随机抽取两名学生聘为学情调查联系人。求第3组中至少有1名学生被聘为学情调查联系人的概率。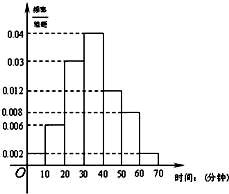
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校共有高一、高二、高三学生2000名,各年级男、女生人数如下图:
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求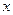 的值;
的值;
(2)现用分层抽样的方法在 全校抽取48名学生,问应在高三年级抽取多少名?
全校抽取48名学生,问应在高三年级抽取多少名?
(3)已知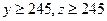 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分l2分)
在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分.已知某选手回答A、B、C三道题正确的概率分别为 、
、 、
、 ,且回答各题时相互之间没有影响.
,且回答各题时相互之间没有影响.
(1) 若此选手可以自由选择答题顺序,求其必答题总分为50分的概率;
(2) 若此选手按A、B、C的顺序答题,求其必答题总分 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com