
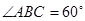 ,
,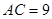 ,
,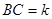 的△ABC恰有一个,那么
的△ABC恰有一个,那么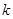 的取值范围是 ;
的取值范围是 ;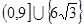
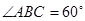 ,
,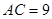 ,
,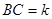 的△ABC恰有一个,则可知解:(1)当AC<BCsin∠ABC,即9<ksin60°,即k>6
的△ABC恰有一个,则可知解:(1)当AC<BCsin∠ABC,即9<ksin60°,即k>6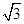 时,三角形无解;(2)当AC=BCsin∠ABC,即12=ksin60°,即k=6
时,三角形无解;(2)当AC=BCsin∠ABC,即12=ksin60°,即k=6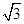 时,三角形有1解;(3)当AC<BCsin∠ABC<BC,即ksin60°<9<k,即9<k<6
时,三角形有1解;(3)当AC<BCsin∠ABC<BC,即ksin60°<9<k,即9<k<6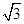 ,三角形有2个解;(4)当0<BC≤AC,即0<k≤9时,三角形有1个解.综上所述:当0<k≤9或k=6
,三角形有2个解;(4)当0<BC≤AC,即0<k≤9时,三角形有1个解.综上所述:当0<k≤9或k=6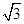 时,三角形恰有一个解.故答案为
时,三角形恰有一个解.故答案为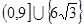


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com