
一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.
(1)求证: 平面ABD⊥平面ACD;
(2)求AD与BC所成的角;
(3)求二面角A—BD—C的大小.

(1)证明略 (2) ![]() (3) 二面角A—BD—C的大小为arctan2
(3) 二面角A—BD—C的大小为arctan2
取BC中点E,连结AE,∵AB=AC,∴AE⊥BC
∵平面ABC⊥平面BCD,∴AE⊥平面BCD,
∵BC⊥CD,由三垂线定理知AB⊥CD.
又∵AB⊥AC,∴AB⊥平面BCD,∵AB![]() 平面ABD.
平面ABD.
∴平面ABD⊥平面ACD。
(2)解: 在面BCD内,过D作DF∥BC,过E作EF⊥DF,交DF于F,由三垂线定理知AF⊥DF,∠ADF为AD与BC所成的角.
设AB=m,则BC=![]() m,CE=DF=
m,CE=DF=![]() m,CD=EF=
m,CD=EF=![]() m
m
![]()

即AD与BC所成的角为arctan![]()
(3)解:∵AE⊥面BCD,过E作EG⊥BD于G,连结AG,由三垂线定理知AG⊥BD,
∴∠AGE为二面角A—BD—C的平面角
∵∠EBG=30°,BE=![]() m,∴EG=
m,∴EG=![]() m
m
又AE=![]() m,∴tanAGE=
m,∴tanAGE=![]() =2,∴∠AGE=arctan2.
=2,∴∠AGE=arctan2.
即二面角A—BD—C的大小为arctan2.
另法(向量法): (略)



科目:高中数学 来源: 题型:
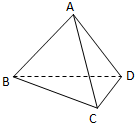 如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,
如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定 AB=AD=2,∠BCD=90°,∠BDC=60°,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,将一副三角板拼成直二面角A-BC-D,其中∠BAC=90°,AB=AC,∠BCD=90°,∠CBD=30°.
如图,将一副三角板拼成直二面角A-BC-D,其中∠BAC=90°,AB=AC,∠BCD=90°,∠CBD=30°.查看答案和解析>>
科目:高中数学 来源:高三数学教学与测试 题型:044
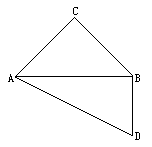
将一副三角板放在同一个平面上组成下图所示的四边形ACBD,△ABC中,∠C=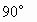 ,AC=BC,△ABD中,∠ABD=
,AC=BC,△ABD中,∠ABD=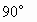 ,∠D=
,∠D=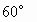 .设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).
.设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).
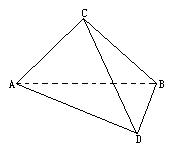
(1)求证:平面ACD⊥平面BCD;
(2)求直线AD和BC所成的角;
(3)求直线AD和平面BCD所成的角;
(4)求平面ACD和平面ABD所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省江南十校高三素质教育联考理科数学试卷(解析版) 题型:填空题
如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述正确的是. _________
① ;②平面BCD的法向量与平面ACD的法向量垂直;③异面直线BC与AD所成的角为60%④四面体有外接球;⑤直线DC与平面ABC所成的角为300
;②平面BCD的法向量与平面ACD的法向量垂直;③异面直线BC与AD所成的角为60%④四面体有外接球;⑤直线DC与平面ABC所成的角为300

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com