
【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为边长为2对的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. 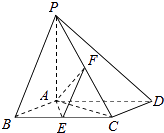
(1)判定AE与PD是否垂直,并说明理由;
(2)若PA=2,求二面角E﹣AF﹣C的余弦值.
【答案】
(1)解:垂直.
证明:由四边形ABCD为菱形,∠ABC=60°,
可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE平面ABCD,
所以PA⊥AE.
而PA平面PAD,AD平面PAD且PA∩AD=A,
所以AE⊥平面PAD,又PD平面PAD,
所以AE⊥PD.
(2)解:由(1)知AE,AD,AP两两垂直,以A为坐标原点,
建立如图所示的空间直角坐标系,又E,F分别为BC,PC的中点,∴A(0,0,0), ![]() ,
, ![]() ,D(0,2,0),P(0,0,2),
,D(0,2,0),P(0,0,2), ![]() ,
,  ,
,
所以 ![]() ,
,  .
.
设平面AEF的一个法向量为 ![]() ,则
,则  ,
,
因此  ,取z1=﹣1,则
,取z1=﹣1,则 ![]() .
.
因为BD⊥AC,BD⊥PA,PA∩AC=A,
所以BD⊥平面AFC,故 ![]() 为平面AFC的一个法向量.
为平面AFC的一个法向量.
又 ![]() ,所以
,所以  .
.
因为二面角E﹣AF﹣C为锐角,所以所求二面角的余弦值为 ![]() .
.

【解析】(1)判断垂直.证明AE⊥BC.PA⊥AE.推出AE⊥平面PAD,然后证明AE⊥PD.(2)由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,求出相关点的坐标,求出平面AEF的一个法向量,平面AFC的一个法向量.通过向量的数量积求解二面角的余弦值.
【考点精析】关于本题考查的直线与平面垂直的性质,需要了解垂直于同一个平面的两条直线平行才能得出正确答案.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:
【题目】设命题P:实数x满足2x2﹣5ax﹣3a2<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=2,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆C满足:①圆心C在射线y=2x(x>0)上; ②与x轴相切;
③被直线y=x+2截得的线段长为 ![]()
(1)求圆C的方程;
(2)过直线x+y+3=0上一点P作圆C的切线,设切点为E、F,求四边形PECF面积的最小值,并求此时 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a,E为侧棱PC的中点,又作DF⊥PB交PB于点F,则PB与平面EFD所成角为( )
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果将函数f(x)=sin2x图象向左平移φ(φ>0)个单位,函数g(x)=cos(2x﹣ ![]() )图象向右平移φ个长度单位后,二者能够完全重合,则φ的最小值为 .
)图象向右平移φ个长度单位后,二者能够完全重合,则φ的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2﹣2x+m=0有两个不相等的实数根;命题q:函数y=(m+2)x﹣1是R上的单调增函数.若“p或q”是真命题,“p且q”是假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() ,动直线
,动直线 ![]()
(1)若动直线l与椭圆C相交,求实数m的取值范围;
(2)当动直线l与椭圆C相交时,证明:这些直线被椭圆截得的线段的中点都在直线3x+2y=0上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的所对的边分别为a,b,c,且a2+b2=ab+c2 .
(Ⅰ) 求tan(C﹣ ![]() )的值;
)的值;
(Ⅱ) 若c= ![]() ,求S△ABC的最大值.
,求S△ABC的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com