
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形.
为矩形.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,确定点
?若存在,确定点![]() 的位置并加以证明.
的位置并加以证明.
【答案】(1)见解析(2)点![]() 为线段
为线段![]() 的中点
的中点
【解析】试题分析:(1)先根据勾股定理得![]() ,再由矩形性质得
,再由矩形性质得![]() ,由线面垂直判定定理得
,由线面垂直判定定理得![]() ,最后根据面面垂直判定定理得结论 (2)根据条件建立空间直角坐标系,设立各点坐标,根据方程组解各平面法向量,根据向量数量积两法向量夹角,最后根据二面角与向量夹角相等或互补关系求点
,最后根据面面垂直判定定理得结论 (2)根据条件建立空间直角坐标系,设立各点坐标,根据方程组解各平面法向量,根据向量数量积两法向量夹角,最后根据二面角与向量夹角相等或互补关系求点![]() 坐标,即得点
坐标,即得点![]() 的位置
的位置
试题解析:(1)证明:由平面几何的知识,易得![]() ,
, ![]() ,
,
又![]() ,所以在
,所以在![]() 中,满足
中,满足![]() ,所以
,所以![]() 为直角三角形,且
为直角三角形,且![]() .
.
因为四边形![]() 为矩形,
为矩形,
所以![]() .
.
由![]() ,
, ![]() ,
, ![]() ,
,
可得 ![]() .
.
又![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.
(2)存在点![]()
![]() 为大小为
为大小为![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
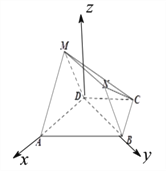
事实上,以![]() 为原点,
为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则![]() ,
, ![]() ,
,
设![]() ,由
,由![]() ,
,
即![]() ,得
,得![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则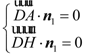 ,即
,即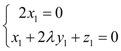 ,
,
不妨设![]() ,取
,取![]() .
.
平面![]() 的一个法向量为
的一个法向量为![]() .
.
![]() 二面角
二面角![]() 为大小为
为大小为![]()
于是 .
.
解得 ![]() 或
或![]() (舍去).
(舍去).
所以当点![]() 为线段
为线段![]() 的中点时,二面角
的中点时,二面角![]() 为大小为
为大小为![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为A,B,C所对边,a+b=4,(2﹣cosA)tan ![]() =sinA.
=sinA.
(1)求边长c的值;
(2)若E为AB的中点,求线段EC的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点是坐标原点![]() ,焦点
,焦点![]() 在
在![]() 轴的正半轴上,过焦点
轴的正半轴上,过焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 两点,且满足
两点,且满足![]() .
.
(1)求抛物线的方程;
(2)已知![]() 为抛物线上一点,若点
为抛物线上一点,若点![]() 位于
位于![]() 轴下方且
轴下方且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来城市“共享单车”的投放在我国各地迅猛发展,“共享单车”为人们出行提供了很大的便利,但也给城市的管理带来了一些困难,现某城市为了解人们对“共享单车”投放的认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 赞成投放的人数 | 赞成投放的人数占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|
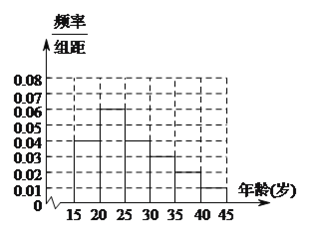
(![]() )求
)求![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取
)在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取![]() 人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
(![]() )在(
)在(![]() )中抽取的
)中抽取的![]() 人中随机选派
人中随机选派![]() 人作为领队,求所选派的
人作为领队,求所选派的![]() 人中第五组至少有一人的概率.
人中第五组至少有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点R(x0 , y0)在D:y2=2px上,以R为切点的D的切线的斜率为 ![]() ,过Γ外一点A(不在x轴上)作Γ的切线AB、AC,点B、C为切点,作平行于BC的切线MN(切点为D),点M、N分别是与AB、AC的交点(如图).
,过Γ外一点A(不在x轴上)作Γ的切线AB、AC,点B、C为切点,作平行于BC的切线MN(切点为D),点M、N分别是与AB、AC的交点(如图).
(1)用B、C的纵坐标s、t表示直线BC的斜率;
(2)设三角形△ABC面积为S,若将由过Γ外一点的两条切线及第三条切线(平行于两切线切点的连线)围成的三角形叫做“切线三角形”,如△AMN,再由M、N作“切线三角形”,并依这样的方法不断作切线三角形…,试利用“切线三角形”的面积和计算由抛物线及BC所围成的阴影部分的面积T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为坐标原点,
为坐标原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在斜率为2的直线![]() ,使得当直线
,使得当直线![]() 与椭圆
与椭圆![]() 有两个不同交点
有两个不同交点![]() 时,能在直线
时,能在直线![]() 上找到一点
上找到一点![]() ,在椭圆
,在椭圆![]() 上找到一点
上找到一点![]() ,满足
,满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:
组数 | 分组 | 认同人数 | 认同人数占 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |
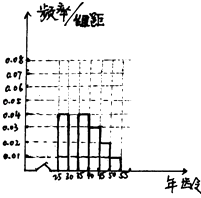
(1)完成所给频率分布直方图,并求n,a,p.
(2)若从[40,45),[45,50)两个年龄段中的“认同”人群中,按分层抽样的方法抽9人参与座谈会,然后从这9人中选2名作为组长,组长年龄在[40,45)内的人数记为ξ,求随机变量ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时生产内径为![]() 的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位:
的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位: ![]() ) ,
) ,
甲:25.44,25.43, 25.41,25.39,25.38
乙:25.41,25.42, 25.41,25.39,25.42.
从生产的零件内径的尺寸看、谁生产的零件质量较高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+1)lnx﹣a(x﹣1).
(1)若函数f(x)在x=e处的切线与y轴相交于点(0,2﹣e),求a的值;
(2)当1<x<2时,求证: ![]() >
> ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com