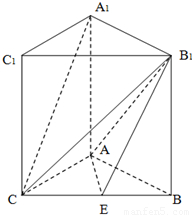
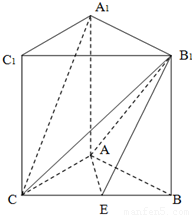
分析:(1)取B
1C
1中点F,连接EF,A
1F,要证明A
1C∥平面AEB
1,只需证明面A
1CF∥面AEB
1,进而转化为线面平行即可;
(2)向量法:建立空间直角坐标系,转化为求平面ACB
1的法向量与向量
的夹角余弦值解决.
解答:
解:(1)取B
1C
1中点F,连接EF,A
1F,
∵FE∥AA
1,FE=AA
1,∴FEAA
1为平行四边形,∴A
1F∥AE,
∵A
1F?面AEB
1,∴A
1F∥面AEB
1,
又CF∥B
1E,CF=B
1E,CF?面AEB
1,
∴CF∥面AEB
1,∴面A
1CF∥面AEB
1,
∴A
1C∥面AEB
1.
(2)∵AC⊥AA
1,AB⊥AA
1,∴∠CAB=θ,
∠CAE=,如图,建立空间直角坐标系,
∴E(0,0,0),A(0,cos
,0),B(sin
,0,0),C(-sin
,0,0),B
1(sin
,0,2),
∴
=(sin
,-cos
,0),
=(-sin
,-cos
,0),
═(2sin
,0,2),
设平面ACB
1的法向量
=(x,y,z),
则-xsin
-ycos
=0,2xsin
+2z=0,
=(cos
,-sin
,-sin
cos
)=(cos
,-sin
,-
sinθ),
∴cos<
,
>=
=
∈(0,
],
所以直线AB与平面ACB
1所成角的正弦值的取值范围为(0,
].
点评:本题考查线面平行的判定、线面角的求解以及面面平行的性质,考查空间向量的坐标运算,考查学生分析问题解决问题的能力.

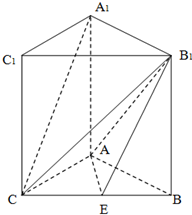 如图,已知矩形AA1B1B中,AA1=2,AB=1,若矩形AA1C1C是矩形AA1B1B绕AA1旋转而成,记二面角B-AA1-C的大小为θ,θ∈(0,π),E是BC的中点.
如图,已知矩形AA1B1B中,AA1=2,AB=1,若矩形AA1C1C是矩形AA1B1B绕AA1旋转而成,记二面角B-AA1-C的大小为θ,θ∈(0,π),E是BC的中点. 解:(1)取B1C1中点F,连接EF,A1F,
解:(1)取B1C1中点F,连接EF,A1F,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案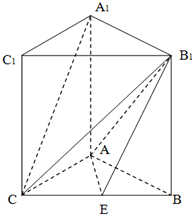 如图,已知矩形AA1B1B中,AA1=2,AB=1,若矩形AA1C1C是矩形AA1B1B绕AA1旋转而成,记二面角B-AA1-C的大小为θ,θ∈(0,π),E是BC的中点.
如图,已知矩形AA1B1B中,AA1=2,AB=1,若矩形AA1C1C是矩形AA1B1B绕AA1旋转而成,记二面角B-AA1-C的大小为θ,θ∈(0,π),E是BC的中点.