解:(Ⅰ)因为S
n=2a
n-3n,所以S
n+1=2a
n+1-3(n+1),
则a
n+1=2a
n+1-2a
n-3,所以a
n+1=2a
n+3,
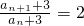
,
数列a
n+3是等比数列,a
1=S
1=3,a
1+3=6,a
n+3=6•2
n-1=3•2
n,
所以a
n=3•2
n-3.
(Ⅱ)
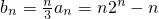
,T
n=2+2•2
2+3•2
3++n•2
n-(1+2++n),
令T
n′=2+2•2
2+3•2
3++n•2
n,①2T
n′=2
2+2•2
3+3•2
4++(n-1)•2
n+n•2
n+1,②
①-②得,-T
n′=2+2
2++2
n-n•2
n+1=-2(1-2
n)-n•2
n+1,T
n′=2+(n-1)•2
n+1,
所以

.
(Ⅲ)设存在s,p,r∈N
*,且s<p<r,使得a
s,a
p,a
r成等差数列,则2a
p=a
s+a
r,即2(3•2
p-3)=3•2
s-3+3•2
r-3
即2
p+1=2
s+2
r,2
p-s+1=1+2
r-s,2
p-s+1,2
r-s为偶数,而1+2
r-s为奇数,
所以2
p+1=2
s+2
r不成立,故不存在满足条件的三项.
分析:(Ⅰ)根据a
n+1=S
n+1-S
n,求得a
n+1=2a
n+3,整理可得
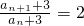
判断出数列a
n+3是等比数列,进而利用等比数列的通项公式求得a
n+3进而求得a
n.
(Ⅱ)把(1)中的a
n代入b
n中,进而利用错位相减法和等差数列的求和公式求得前n项的和.
(Ⅲ)设存在s,p,r∈N
*,且s<p<r,使得a
s,a
p,a
r成等差数列,根据等差中项的性质可知2a
p=a
s+a
r,利用(1)中的a
n展开得2
p+1=2
s+2
r,2
p-s+1=1+2
r-s,进而根据2
p-s+1,2
r-s为偶数,而1+2
r-s为奇数,判断出假设不成立.故可知不存在这样的三项.
点评:本题主要考查了数列的求和问题.考查了学生综合分析问题和解决问题的能力.

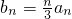 ,求数列bn的前n项和Tn;
,求数列bn的前n项和Tn;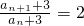 ,
,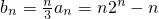 ,Tn=2+2•22+3•23++n•2n-(1+2++n),
,Tn=2+2•22+3•23++n•2n-(1+2++n), .
.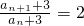 判断出数列an+3是等比数列,进而利用等比数列的通项公式求得an+3进而求得an.
判断出数列an+3是等比数列,进而利用等比数列的通项公式求得an+3进而求得an.
