解:(Ⅰ)已知数列{a
n}满足a
1=1,a
2=3,且
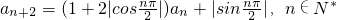
,
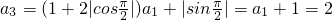
,
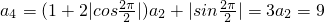
,…(2分)
(Ⅱ)①设n=2k,k∈N
*,
∵
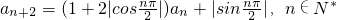
,
又a
2=3,
∴
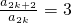
.
∴当k∈N
*时,数列{a
2k}为等比数列.
∴a
2k=a
2•3
k-1=3
k.
②设n=2k-1,k∈N
*.…(5分)
由
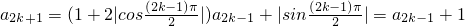
,
∴a
2k+1-a
2k-1=1.
∴当k∈N
*时,数列{a
2k-1}为等差数列.
∴a
2k-1=a
1+(k-1)•1=k.…(8分)
(Ⅲ)b
k=a
2k+(-1)
k-1λ•2
k-1=3
k+(-1)
k-1λ•2
k∴b
k+1-b
k=3
k+1+(-1)
kλ•2
k+1-3
k-(-1)
k-1λ•2
k
=2•3
k+(-1)
kλ(2
k+1+2
k)
=2•3
k+(-1)
kλ•3•2
k.
由题意,对任意k∈N
*都有b
k+1>b
k成立,
∴b
k+1-b
k=2•3
k+(-1)
kλ•3•2
k>0对任意k∈N
*恒成立,
∴2•3
k>(-1)
k-1λ•3•2
k对任意k∈N
*恒成立.
①当k为奇数时,
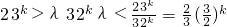
对任意k∈N
*恒成立.
∵k∈N
*,且k为奇数,
∴
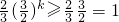
.
∴λ<1.
②当k为偶数时,

对任意k∈N
*恒成立.
∵k∈N
*,且k为偶数,
∴
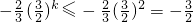
.∴

.
综上,有
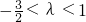
.
∵λ为非零整数,∴λ=-1.…(14分)
分析:已知数列{a
n}满足a
1=1,a
2=3,且
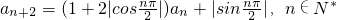
,
(Ⅰ)由题设条件,分别令n=1和n=2,能求出a
3,a
4.
(Ⅱ)设n=2k,k∈N
*,由题设能导出
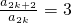
.由此能求出a
2k.设n=2k-1,k∈N
*.由
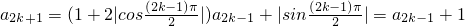
,知a
2k+1-a
2k-1=1.由此能求出a
2k-1.
(Ⅲ)b
k=a
2k+(-1)
k-1λ•2
k-1=3
k+(-1)
k-1λ•2
k,b
k+1-b
k=3
k+1+(-1)
kλ•2
k+1-3
k-(-1)
k-1λ•2
k=2•3
k+(-1)
kλ(2
k+1+2
k)=2•3
k+(-1)
kλ•3•2
k.由题意,对任意k∈N
*都有b
k+1>b
k成立,由此能确定λ的值,使得对任意(k∈N
+)都有b
k+1>b
k成立.
点评:本题考查数列与不等式的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

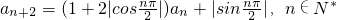 ,
,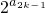 (λ为非零整数),试确定λ的值,使得对任意(k∈N+)都有bk+1>bk成立.
(λ为非零整数),试确定λ的值,使得对任意(k∈N+)都有bk+1>bk成立.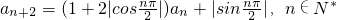 ,
,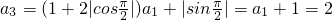 ,
,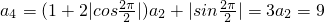 ,…(2分)
,…(2分)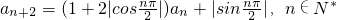 ,
,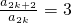 .
.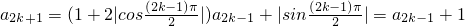 ,
,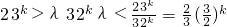 对任意k∈N*恒成立.
对任意k∈N*恒成立.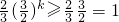 .
. 对任意k∈N*恒成立.
对任意k∈N*恒成立.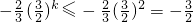 .∴
.∴ .
.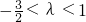 .
.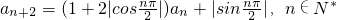 ,
,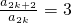 .由此能求出a2k.设n=2k-1,k∈N*.由
.由此能求出a2k.设n=2k-1,k∈N*.由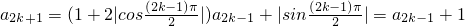 ,知a2k+1-a2k-1=1.由此能求出a2k-1.
,知a2k+1-a2k-1=1.由此能求出a2k-1.
