
已知函数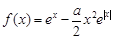 .
.
(Ⅰ)若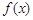 是
是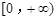 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(Ⅱ)证明:当a≥1时,证明不等式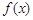 ≤x+1对x∈R恒成立;
≤x+1对x∈R恒成立;
(Ⅲ)对于在(0,1)中的任一个常数a,试探究是否存在x0>0,使得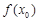 >x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
(I)a的取值范围为a≤0;(Ⅱ)详见解析;(Ⅲ)可找到一个常数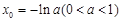 ,使得
,使得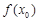 >x0+1成立.
>x0+1成立.
解析试题分析:(I) 时,
时, ,求导得
,求导得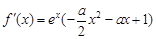 .由题意,
.由题意,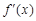 ≥0在
≥0在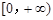 上恒成立.因为ex>0恒成立,故只需
上恒成立.因为ex>0恒成立,故只需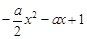 ≥0在
≥0在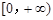 上恒成立,结合抛物线的图象即可得a的取值范围;(Ⅱ)由题知f(x)≤x+1即为
上恒成立,结合抛物线的图象即可得a的取值范围;(Ⅱ)由题知f(x)≤x+1即为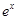 -
-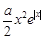 ≤x+1.由于含有
≤x+1.由于含有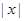 ,故分
,故分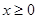 和
和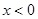 两种情况讨论.①在x≥0时,要证明
两种情况讨论.①在x≥0时,要证明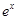 -
-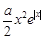 ≤x+1成立,可变为证1≤
≤x+1成立,可变为证1≤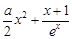 成立,这样只需利用导数求
成立,这样只需利用导数求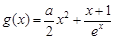 的最小值即可,求导得
的最小值即可,求导得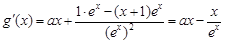 ,易得
,易得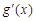 ≥0,从而g(x)≥g(0)=1.注:直接证
≥0,从而g(x)≥g(0)=1.注:直接证 也可,只是需要求两次导数.
也可,只是需要求两次导数.
②在x≤0时,要证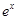 -
-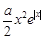 ≤x+1成立,可变为证1≤
≤x+1成立,可变为证1≤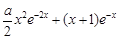 成立,这样只需利用导数求
成立,这样只需利用导数求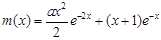 的最小值即可.
的最小值即可.
(Ⅲ)要使f(x0)>x0+1成立,即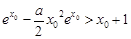 .如果变为
.如果变为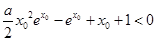 ,那么求导后式子很复杂,故尝试作其它的变形.
,那么求导后式子很复杂,故尝试作其它的变形.
变形为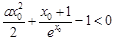 ,要找一个x0>0使该不等式成立,只需找到函数
,要找一个x0>0使该不等式成立,只需找到函数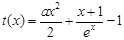 的最小值,满足
的最小值,满足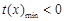 即可.这利用导数就容易解决了.
即可.这利用导数就容易解决了.
试题解析:(I)∵ 时,
时, ,
,
∴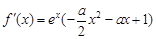 .
.
由题意,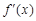 ≥0在
≥0在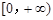 上恒成立,
上恒成立,
当a=0时,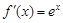 >0恒成立,即满足条件.
>0恒成立,即满足条件.
当a≠0时,要使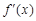 ≥0,而ex>0恒成立,
≥0,而ex>0恒成立,
故只需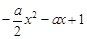 ≥0在
≥0在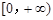 上恒成立,即
上恒成立,即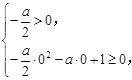 解得a<0.
解得a<0.
综上,a的取值范围为a≤0. 4分
(Ⅱ)由题知f(x)≤x+1即为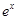 -
-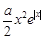 ≤x+1.
≤x+1.
①在x≥0时,要证明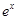 -
-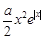 ≤x+1成立,
≤x+1成立,
只需证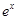 ≤
≤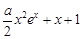 ,即证1≤
,即证1≤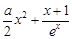 , ①
, ①
令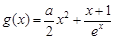 ,得
,得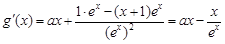 ,
,
整理得 ,
,
∵x≥0时,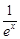 ≤1,结合a≥1,得
≤1,结合a≥1,得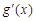 ≥0,
≥0,
∴ 为在
为在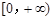 上是增函数,故g(x)≥g(0)=1,从而①式得证.
上是增函数,故g(x)≥g(0)=1,从而①式得证.
②在x≤0时,要使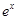 -
-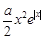 ≤x+1成立,
≤x+1成立,
只需证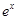 ≤
≤ ,即证1≤
,即证1≤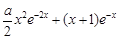 , ②
, ②
令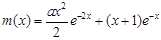 ,得
,得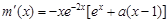 ,
,
而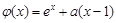 在x≤0时为增函数,
在x≤0时为增函数,
故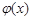 ≤
≤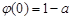 ≤0,从而
≤0,从而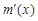 ≤0,
≤0,
∴m(x)在x≤0时为减函数,则m(x)≥m(0)=1,从而②式得证.
综上所述,原不等式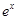 -
-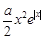 ≤x+1即f(x)≤x+1在a≥1时恒成立. 10分
≤x+1即f(x)≤x+1在a≥1时恒成立. 10分
(Ⅲ)要使f(x0)>x0+1成立,即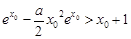 ,
,
变形为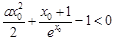 , ③
, ③
要找一个x0>0使③式成立,只


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=ln x+ -1.
-1.
(1)求函数f(x)的单调区间;
(2)设m∈R,对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
(1)求 的最小值;
的最小值;
(2)设 ,
, .
.
(ⅰ)证明:当 时,
时, 的图象与
的图象与 的图象有唯一的公共点;
的图象有唯一的公共点;
(ⅱ)若当 时,
时, 的图象恒在
的图象恒在 的图象的上方,求实数
的图象的上方,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经调查统计,某种型号的汽车在匀速行驶中,每小时的耗油量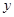 (升)关于行驶速度
(升)关于行驶速度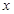 (千米/时)的函数可表示为
(千米/时)的函数可表示为 .已知甲、乙两地相距
.已知甲、乙两地相距 千米,在匀速行驶速度不超过
千米,在匀速行驶速度不超过 千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为
千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为 (升).
(升).
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)讨论函数 的单调性,当
的单调性,当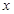 为多少时,耗油量
为多少时,耗油量 为最少?最少为多少升?
为最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
① 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数;
② 是偶函数;
是偶函数;
③ 在x=0处的切线与直线
在x=0处的切线与直线 y=x+2垂直.
y=x+2垂直.
(1)求函数 =
= 的解析式;
的解析式;
(2)设g(x)= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两地相距1000 ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的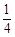 倍,固定成本为a元.
倍,固定成本为a元.
(1)将全程运输成本y(元)表示为速度v( )的函数,并指出这个函数的定义域;
)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,货车应以多大的速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com