
甲、乙两地相距skm,汽车从甲地匀速行驶到乙地,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成,可变部分与速度x(km/h)的平方成正比,比例系数为a,固定部分为b元,请问,是不是汽车的行驶速度越快,其全程运输成本越小?如果不是,那么为了使全程运输成本最小,汽车应以多大的速度行驶?
解:设汽车运输成本为y元,依题意得汽车运输成本y与汽车行驶速度x之间的关系为:y=b· ∴y=s(ax+ 设x1,x2∈(0,+∞),且x1<x2,则 f(x1)-f(x2)=s[(ax1+ =s[a(x1-x2)+ = = ∵x1,x2>0,且x1<x2 ∴x1x2>0,a(x1-x2)<0 ∴当x1,x2∈(0, 当x1,x2∈[ 综上所述,我们看到函数y=s(ax+
|


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:高中数学 来源: 题型:044
甲、乙两地相距
skm,汽车从甲地匀速行驶到乙地,速度不超过ckm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成.可变部分与速度v(km/h)的平方成正比,且比例系数为b,固定部分为a元.(1)
把全程运输成本y(元)表示为速度的函数,并指出这个函数的定义域;(2)
为了使全程运输成本最小,汽车应以多大速度行驶?查看答案和解析>>
科目:高中数学 来源: 题型:044
甲、乙两地相距
skm,汽车从甲地匀速行驶到乙地,速度不得超过ckm/h.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(单位:km/h)的平方成正比,且比例系数为b;固定部分为a元(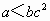 ).为了使全程运输成本最小,汽车应以多大速度行驶?
).为了使全程运输成本最小,汽车应以多大速度行驶?查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
甲、乙两地相距skm,汽车从甲地匀速行驶到乙地,速度不超过ckm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成.可变部分与速度v(km/h)的平方成正比,且比例系数为b,固定部分为a元.
(1)把全程运输成本y(元)表示为速度的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
甲、乙两地相距skm,汽车从甲地匀速行驶到乙地,速度不得超过ckm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度v(km/h)的平方成正比,比例系数为b;固定部分为a元.
(1)把全部运输成本y(元)表示为速度v(km/h)的函数,并指出定义域.
(2)为使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com