
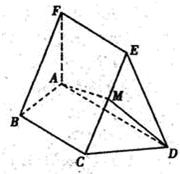
 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE= AD
AD AP
AP  BC
BC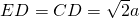 …(5分)
…(5分) AP
AP  BC,所以FA∥EP,可得EP⊥平面ABCD,所以EP⊥PC,EP⊥AD,再结合直角三角形的性质可得:ED=CD,进而得到:DM⊥CE,又BF∥EC,所以DM⊥BF.
BC,所以FA∥EP,可得EP⊥平面ABCD,所以EP⊥PC,EP⊥AD,再结合直角三角形的性质可得:ED=CD,进而得到:DM⊥CE,又BF∥EC,所以DM⊥BF.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.查看答案和解析>>
科目:高中数学 来源: 题型:
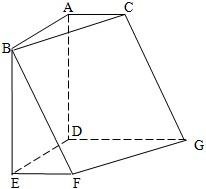
 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年辽宁省鞍山一中高考数学五模试卷(理科)(解析版) 题型:解答题
 ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.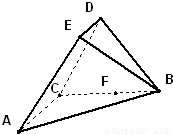
查看答案和解析>>
科目:高中数学 来源:2012年高考数学预测试卷2(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com