练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图1所示为一平面图形的直观图，则此平面图形可能是图2中的（　　）

     

    【答案】

    C

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定（平面图如图所示），如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80
    元/米2，水池所有墙的厚度忽略不计．
    （1）试设计污水处理池的长和宽，使总造价最低，并求出最低总造价；
    （2）若由于地形限制，该池的长和宽都不能超过16米，试设计污水池的长和宽，使总造价最低，并求出最低总造价．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

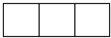    精英家教网某工厂拟建一座平面图（如图所示）为矩形且面积为200m2的三级污水处理池，由于地形限制，长、宽都不能超过16m．如果池外周壁建造单价为每米400元，中间两条隔墙建造单价为每米248元，池底建造单价为每平方米80元（池壁厚度忽略不计，且池无盖）．
    （1）写出总造价y（元）与污水处理池长x（m）的函数关系式，并指出其定义域；
    （2）求污水处理池的长和宽各为多少时，污水处理池的总造价最低？并求出最低总造价．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

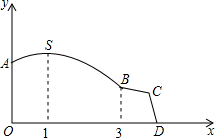    精英家教网安通驾校拟围着一座山修建一条环形训练道路OASBCD，道路的平面图如图所示（单位：km），已知曲线ASB为函数y=Asin（ωx+φ）（A＞0，0＜ω＜1，|φ|＜
    π
    2
    ），x∈[0，3]的图象，且最高点为S（1，2），折线段AOD为固定线路，其中AO=
    		3
    ，OD=4，折线段BCD为可变线路，但为保证驾驶安全，限定∠BCD=120°．
    （1）求A，ω，φ的值；
    （2）应如何设计，才能使折线段道路BCD最长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定（平面图如图所示），如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80元/米2，水池所有墙的厚度忽略不计．
    （1）设污水处理池的宽为x，求总造价f（x）的函数解析式；
    （2）要使总造价最低，求最低总造价及对应污水处理池的长和宽．

    查看答案和解析>>

    科目：高中数学 来源：2013年山东省菏泽市鄄城一中高考数学三模试卷（文科）（解析版） 题型：解答题

    某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定（平面图如图所示），如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80
    元/米2，水池所有墙的厚度忽略不计．
    （1）试设计污水处理池的长和宽，使总造价最低，并求出最低总造价；
    （2）若由于地形限制，该池的长和宽都不能超过16米，试设计污水池的长和宽，使总造价最低，并求出最低总造价．

    查看答案和解析>>

    同步练习册答案