
已知点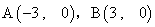 ,动点P 满足:|PA|=2|PB|.
,动点P 满足:|PA|=2|PB|.
(1)若点P的轨迹为曲线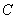 ,求此曲线的方程;
,求此曲线的方程;
(2)若点Q在直l1: x+y+3=0上,直线l2经过点Q且与曲线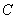 只有一个公共点M,求|QM|的最小值。
只有一个公共点M,求|QM|的最小值。
科目:高中数学 来源: 题型:
动点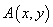 在圆
在圆 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间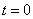 时,点
时,点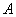 的坐标是
的坐标是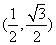 ,则当
,则当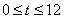 时,动点
时,动点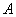 的纵坐标
的纵坐标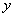 关于
关于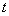 (单位:秒)的函数的单调递增区间是 ( )
(单位:秒)的函数的单调递增区间是 ( )
A. 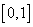 B.
B.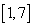 C.
C.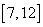 D.
D.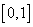 和
和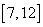
查看答案和解析>>
科目:高中数学 来源: 题型:
设P为曲线C:y= +2
+2 +3上的点,且曲线C在点P处切线倾斜角的取值范围是
+3上的点,且曲线C在点P处切线倾斜角的取值范围是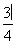 ,
, ),则点P横坐标的取值范围为
),则点P横坐标的取值范围为
A.-1,- 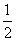 B.-
B.-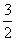 ,-1) C.0,1) D.
,-1) C.0,1) D.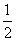 ,1
,1
查看答案和解析>>
科目:高中数学 来源: 题型:
给出以下命题:
①对于平面几何中的命题:“夹在两条平行线之间的平行线段相等”,在立体几何中,类比上述命题,可以得到命题:“夹在两个平行平面间的平行线段相等”.
② =2;
=2;
③已知函数f(x)=x3-3x的图象与直线y=a有相异三个公共点,则a的取值范围是
(-2,2)
其中正确命题是
A.①②③ B.①② C.①③ D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为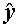 =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心 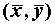
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com