
| 1 | 3 |
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 3 3 |
| 1 |
| 3 |
| 7 |
| 27 |
| 2 |
| 3 |
| 8 |
| 27 |
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| p |
|
|
|
|
| 8 |
| 27 |
| 4 |
| 9 |
| 2 |
| 9 |
| 1 |
| 27 |


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
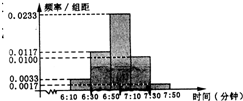 (2012•莆田模拟)小明家订了一份《湄洲日报》,暑假期间他收集了每天报纸送达的时间的数据,并绘制成频率分布直方图如图所示.
(2012•莆田模拟)小明家订了一份《湄洲日报》,暑假期间他收集了每天报纸送达的时间的数据,并绘制成频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,他们三人的投票相互没有影响,规定:若投票结果中至少有两张“参加“票,则决定参加该理财项目;否则,放弃该理财项目.
,他们三人的投票相互没有影响,规定:若投票结果中至少有两张“参加“票,则决定参加该理财项目;否则,放弃该理财项目.查看答案和解析>>
科目:高中数学 来源:2011年陕西省宝鸡市高三质量检测数学试卷2(理科)(解析版) 题型:解答题
 ,他们三人的投票相互没有影响,规定:若投票结果中至少有两张“参加“票,则决定参加该理财项目;否则,放弃该理财项目.
,他们三人的投票相互没有影响,规定:若投票结果中至少有两张“参加“票,则决定参加该理财项目;否则,放弃该理财项目.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com