
已知向量a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三个向量共面,则实数λ等于( )
A.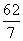 B.
B.
C.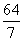 D.
D.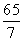
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
下列为真命题的是( )
A.△ABC⊂α,△A′B′C′⊂β,且△ABC∽△A′B′C′,则α∥β
B.α内有两条直线平行于β,则α∥β
C.α内有无数个点与β的距离相等,则α∥β
D.△ABC的三边都平行于平面α,则平面ABC∥α
查看答案和解析>>
科目:高中数学 来源: 题型:
在三棱柱ABC A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是( )
A.30° B.45°
C.60° D.90°
图K433
查看答案和解析>>
科目:高中数学 来源: 题型:
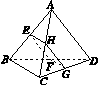
如图K437所示,在正三棱锥A BCD中,∠BAC=30°,AB=a,平行于AD,BC的截面EFGH分别交AB,BD,DC,CA于E,F,G,H.
(1)判定四边形EFGH的形状,并说明理由.
(2)设P是棱AD上的点,当AP为何值时,平面PBC⊥平面EFGH?请给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
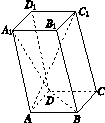
如图K445所示,已知平行六面体ABCD A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,∠A1AB=∠A1AD=120°.
(1)求线段AC1的长;
(2)求异面直线AC1与A1D所成角的余弦值;
(3)证明:AA1⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
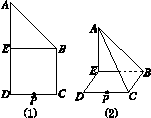
在四边形ABCD中,BC∥AD,BC⊥CD,AD=4,BC=CD=2,E,P分别为AD,CD的中点(如图K4510(1)所示),将△ABE沿BE折起,使二面角A BE C为直二面角,如图(2),在线段AE上,是否存在一点M,使得PM∥平面ABC?若存在,请指出点M的位置,并证明你的结论;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com