练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设数列｛a｝的首项a=1,前n项和S满足关系式：3tS-(2t+3)S=3t(t>0,n=2,3,4…).(1)求证：数列｛a｝是等比数列；(2)设数列｛a｝的公比为f(t),若数列｛b｝满足：b=1,b=f()(n=2,3,4…),求;(3) 对于（2）中的数列｛b｝，求bb-bb+bb-…+(-1) bb的和。

    (Ⅰ) 见解析   (Ⅱ)   （Ⅲ）bb-bb+bb-…+(-1) bb=


    解析:

    ：(1)由S= a=1，S= a+a=1+a,

    3t(1+a)-(2t+3)=3t, ∴a=∴=

    又3tS-(2t+3)S=3t，3tS-(2t+3)S=3t两式相减

    得3ta-(2t+3)a=0 ∴=( n=,3,4…)

    ∴｛a｝是首项a=1,公比为等比数列.

    (2)∵f(t)==+, ∴b=f()=+b

    ｛b｝是首项为1,公差为的等差数列，∴b=1+(n-1)=

    又由(1)知a=(),lga=(n-1)lg

    ==

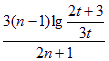    (3) 由b=,可知｛b｝，｛b｝分别是首项为1和,公差均为的等差数列，∴b=，b=     当n=2m(m=1,2,3, …)时,

    bb-bb+bb-bb+…+bb-bb

    =b(b-b)+b(b-b)+…+b(b-b)=-(b+b+…+b)

    =-=-=-

    当n=2m-1(m=1,2,3, …)时,

    bb-bb+bb-bb+…-bb+bb

    =-+ bb=-+

    ==

    ∴bb-bb+bb-…+(-1) bb=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    数列{an}的首项为1，前n项和是Sn，存在常数A，B使an+Sn=An+B对任意正整数n都成立．
    （1）设A=0，求证：数列{an}是等比数列；
    （2）设数列{an}是等差数列，若p＜q，且
    1
    Sp
    +
    1
    Sq
    =
    1
    S11
    ，求p，q的值．
    （3）设A＞0，A≠1，且
    an
    an+1
    ≤M    对任意正整数n都成立，求M的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}的前n项和为Sn，若对于任意的n∈N*，都有Sn=2an-3n．
    （1）求数列{an}的首项a1与递推关系式：an+1=f（an）；
    （2）先阅读下面定理：“若数列{an}有递推关系an+1=Aan+B，其中A、B为常数，且A≠1，B≠0，则数列{an-
    B1-A
    }    是以A为公比的等比数列．”请你在第（1）题的基础上应用本定理，求数列{an}的通项公式；
    （3）求数列{an}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}的首项a1=1，a2=3，前n项和为Sn，且Sn+1、Sn、Sn-1（n≥2）分别是直线l上的点A、B、C的横坐标，
    AB
    =
    2an+1
    an
    BC
    ，设b1=1，bn+1=log2（an+1）+bn．
    （1）判断数列{an+1}是否为等比数列，并证明你的结论；
    （2）设cn=
    4
    bn+1-1
    n+1
    anan+1
    ，证明：
    n
    k=1
    Ck＜1    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知公差不为0的等差数列{an}的首项a1=a（a∈R），设数列{an}的前n项和为Sn，且a1、a2、a4恰为等比数列{bn}的前三项．
    （1）求数列{an}的通项公式及Sn；
    （2）当n≥2时，比较An=
    1
    S1
    +
    1
    S2
    +…+
    1
    Sn
    与Bn=
    1
    b1
    +
    1
    b2
    +…+
    1
    bn
    的大小．（可使用结论：n≥2时，2n＞n+1）

    查看答案和解析>>

    同步练习册答案