
分析 (1)利用等差数列的定义及其通项公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:(1)由an+2=2an+1-an,∴an+2+an=2an+1,∴{an}为等差数列,
设{an}的首项为a1,公差为d,则$\left\{{\begin{array}{l}{{a_1}+2d=9}\\{{a_1}+5d=18}\end{array}}\right.$,解之得$\left\{{\begin{array}{l}{{a_1}=3}\\{d=3}\end{array}}\right.$,
∴{an}的通项公式为an=3n.
(2)${C_n}=\frac{2}{3n(n+1)}=\frac{2}{3}(\frac{1}{n}-\frac{1}{n+1})$,
${T_n}=\frac{2}{3}[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n}-\frac{1}{n+1})]$=$\frac{2}{3}(1-\frac{1}{n+1})=\frac{2n}{3(n+1)}$.
点评 本题考查了等差数列的定义及其通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,$\sqrt{2}$) | C. | (0,2) | D. | (0,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
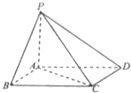 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,AD=2,AB=PA=1,且PA⊥平面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,AD=2,AB=PA=1,且PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M+m=4 | B. | M+m=3 | C. | M-m=4 | D. | M-m=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{64}{81}$ | C. | $\frac{17}{81}$ | D. | $\frac{1}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (log2$\frac{3}{2}$,1) | B. | (log2$\frac{2}{3}$,1) | C. | ($\frac{2}{3}$,1) | D. | [0,$\frac{3}{4}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com