
| A. | (log2$\frac{3}{2}$,1) | B. | (log2$\frac{2}{3}$,1) | C. | ($\frac{2}{3}$,1) | D. | [0,$\frac{3}{4}$] |
分析 这是一个分段函数,从x0∈[0,1)入手,依次表达出里层的解析式,最后得到4-2•2x0∈[0,1),解不等式得到结果.
解答 解:f(x)=$\left\{\begin{array}{l}{{2}^{x},x∈[0,1)}\\{4-2x,x∈[1,2]}\end{array}\right.$,
x0∈[0,1),则f(x0)=2x0,
则f[f(x0)]=4-2•2x0∈[0,1),
即为$\frac{3}{2}$<2x0≤2,
解得log2$\frac{3}{2}$<x0≤1,
由0≤x0<1,
可得log2$\frac{3}{2}$<x0<1,
故选:A.
点评 本题考查元素与集合间的关系,考查分段函数,解题的关键是看清自变量的范围,代入适合的代数式.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{\sqrt{2}}{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
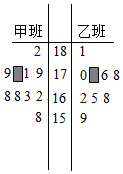 随机抽取某中学高三年级甲,乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图,其中甲,乙两班各有一个数据被污损.
随机抽取某中学高三年级甲,乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图,其中甲,乙两班各有一个数据被污损.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
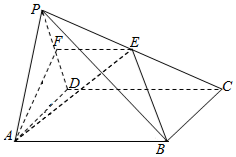 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠DAB=60°.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠DAB=60°.点E是棱PC的中点,平面ABE与棱PD交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE、BE,∠APE的平分线与AE、BE分别交于点C、D,其中∠AEB=30°.
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE、BE,∠APE的平分线与AE、BE分别交于点C、D,其中∠AEB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
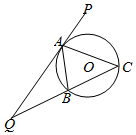 如图,△ABC的外接圆为⊙O,延长CB至Q,延长QA至P,使得QA成为QC,QB的等比中项.
如图,△ABC的外接圆为⊙O,延长CB至Q,延长QA至P,使得QA成为QC,QB的等比中项.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
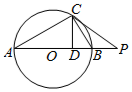 如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,CD⊥AB于D,求证:$\frac{CD}{CP}$=$\frac{DB}{BP}$.
如图,已知点P为Rt△ABC的斜边AB的延长线上一点,且PC与Rt△ABC的外接圆相切,CD⊥AB于D,求证:$\frac{CD}{CP}$=$\frac{DB}{BP}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com