
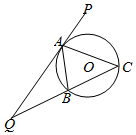
 如图,△ABC的外接圆为⊙O,延长CB至Q,延长QA至P,使得QA成为QC,QB的等比中项.
如图,△ABC的外接圆为⊙O,延长CB至Q,延长QA至P,使得QA成为QC,QB的等比中项.分析 (Ⅰ)由已知可得QC•QB=QA2,即$\frac{QC}{QA}=\frac{QA}{QB}$,可得△QCA∽△QAB,进而∠QAB=QCA,根据弦切角定理的逆定理可得QA为⊙O的切线;
(Ⅱ)根据弦切角定理可得AC=BC=6,结合(I)中结论,可得QC:QA=AC:AB=6:4,进而得到答案.
解答 (Ⅰ)证明:∵QA成为QC,QB的等比中项,
∴QC•QB=QA2,
于是$\frac{QC}{QA}=\frac{QA}{QB}$,
∴△QCA∽△QAB,
∴∠QAB=QCA,
根据弦切角定理的逆定理可得QA为⊙O的切线,(5分)
(Ⅱ)解:∵QA为⊙O的切线,
∴∠PAC=∠ABC,而AC恰好为∠BAP的平分线,
∴∠BAC=∠ABC,
于是AC=BC=6,
∴QC2-QA2=6QC,①
又由△QCA∽△QAB得
QC:QA=AC:AB=3:2,②
联合①②消掉QC,得QA=7.2.(10分)
点评 本题考查的知识点是弦切角定理及其逆定理,圆的切线的判定与性质,三角形相似的判定与性质,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{64}{81}$ | C. | $\frac{17}{81}$ | D. | $\frac{1}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (log2$\frac{3}{2}$,1) | B. | (log2$\frac{2}{3}$,1) | C. | ($\frac{2}{3}$,1) | D. | [0,$\frac{3}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
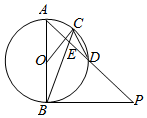 如图随时,AB是⊙O的直径,C,D是⊙O上的两点,OC⊥AD.过点B作⊙O的切线PB交AD的延长线于点P,连接BC交AD于点E.
如图随时,AB是⊙O的直径,C,D是⊙O上的两点,OC⊥AD.过点B作⊙O的切线PB交AD的延长线于点P,连接BC交AD于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ρ=1 | B. | ρsinθ=1 | C. | ρcosθ=1 | D. | ρ=2sinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$$<\frac{f(2)}{f(4)}$$<\frac{1}{2}$ | B. | $\frac{1}{4}<\frac{f(2)}{f(4)}$$<\frac{1}{3}$ | C. | $\frac{1}{8}$$<\frac{f(2)}{f(4)}$$<\frac{1}{4}$ | D. | $\frac{1}{16}$$<\frac{f(2)}{f(4)}$$<\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
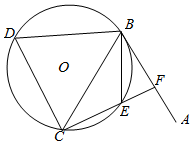 如图所示,直线AB为圆O的切线,切点为B,点C在圆O上,∠ABC的平分线BE交圆O于点E,DB垂直BE交圆O于点D.
如图所示,直线AB为圆O的切线,切点为B,点C在圆O上,∠ABC的平分线BE交圆O于点E,DB垂直BE交圆O于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com