【题目】已知函数
有唯一零点，则a=
A. 
B. 
C. 
D. 
【答案】A
【解析】分析：通过转化可知问题等价于函数y=1﹣（x﹣1）2的图象与y=a（
+
）的图象只有一个交点求a的值．分a=0、a＜0、a＞0三种情况，结合函数的单调性分析可得结论．
详解：因为f（x）
=﹣8+2（x﹣2）2+a（+）=0，
所以函数f（x）有唯一零点等价于方程8﹣2（x﹣2）2= a（+）有唯一解，
等价于函数y=8﹣2（x﹣2）2的图象与y= a（+）的图象只有一个交点．
当a=0时，f（x）=
≥﹣8，此时有两个零点，矛盾；
当a＜0时，由于y=8﹣2（x﹣2）2在（﹣∞，2）上递增、在（2，+∞）上递减，
且a（+）在（﹣∞，2）上递增、在（2，+∞）上递减，
所以函数y=8﹣2（x﹣2）2的图象的最高点为A（2，8），y= a（+）的图象的最高点为B（2，2a），
由于2a＜0＜8，此时函数y=8﹣2（x﹣2）2的图象与a（+）的图象有两个交点，矛盾；
当a＞0时，由于y=8﹣2（x﹣2）2在（﹣∞，2）上递增、在（2，+∞）上递减，
且y= a（+）在（﹣∞，2）上递减、在（2，+∞）上递增，
所以函数y=8﹣2（x﹣2）2的图象的最高点为A（2，8），y= a（+）的图象的最低点为B（2，2a），
由题可知点A与点B重合时满足条件，即2a=8，即a=
，符合条件；
综上所述，a=，
故选：A．
科目：高中数学 来源： 题型：
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD的中点,PE⊥BE,PA=PD=AD=2,AB=
.
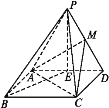
(1)求证:PB∥平面MAC.
(2)求证:平面MAC⊥平面PBE.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
（a>b>0），四点P1（1,1），P2（0,1），P3（–1， 
），P4（1， 
）中恰有三点在椭圆C上.
（1）求C的方程；
（2）设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为–1，证明：l过定点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将函数
的图象向左平移
个单位长度，再向上平移1个单位长度，得到函数g（x）的图象，则函数g（x）具有性质_____．（填入所有正确结论的序号）
①最大值为
，图象关于直线
对称；
②图象关于y轴对称；
③最小正周期为π；
④图象关于点
对称．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线C的顶点为原点，焦点F与圆
的圆心重合.
（1）求抛物线C的标准方程；
（2）设定点
，当P点在C上何处时，
的值最小，并求最小值及点P的坐标；
（3）若弦
过焦点
，求证：
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列两个命题：命题p1：a，b∈（0，+∞），当a+b=1时， 
+ 
=4；命题p2：函数y=ln 
是偶函数．则下列命题是真命题的是（ ）
A.p1∧p2
B.p1∧（￢p2）
C.（￢p1）∨p2
D.（￢p1）∨（￢p2）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
