
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%把握判定变量A,B有关联. |
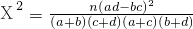 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.) | 喜爱运动 | 不喜爱运动 | 合计 | |
| 男 | 10 | 6 | 16 |
| 女 | 6 | 8 | 14 |
| 合计 | 16 | 14 | 30 |
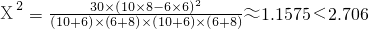 (10分)
(10分)

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%把握判定变量A,B有关联. |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%把握判定变量A,B有关联. |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省宝鸡市金台区高二(下)期中数学试卷(文科)(解析版) 题型:解答题
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%把握判定变量A,B有关联. |
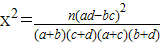 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com