解:(1)∵f(x)=
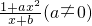
是奇函数,
∴f(-x)+f(x)=
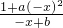
+

=(1+ax
2)•
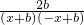
=0,
∴b=0;
∴f(x)=
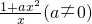
,又f(x)的图象经过点(1,3),
∴
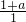
=3,
∴a=2;
∴f(x)=2x+

;
(2)当x>0时,f(x)=2x+

在[

,+∞)上单调递增.
证明:令

≤x
1<x
2,
则f(x
2)-f(x
1)=2(x
2-x
1)+(

-

)=(x
2-x
1)(2-
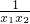
),
∵

≤x
1<x
2,
∴0<
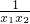
<2,于是2-
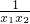
>0,
∴(x
2-x
1)(2-
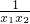
)>0,
∴f(x
2)>f(x
1).
∴当x>0时,f(x)=2x+

在[

,+∞)上单调递增.
(3)∵f(x)=2x+

(x>0),
∴f′(x)=2-

,由f′(x)≥0可得x≥

,由f′(x)<0可得0<x<

,
∴f(x)=2x+

在[

,+∞)上单调递增,在(0,

]上单调递减.
∴f(x)=2x+

在x=

处取到最小值2

,
∴当x>0时f(x)=2x+

的值域为:[2

,+∞).
分析:(1)由f(-x)+f(x)=0可求得b=0;又f(x)的图象经过点(1,3),从而可求得a;
(2)当x>0时,f(x)=2x+

在[

,+∞)上单调递增,利用单调性的定义证明即可;
(3)可利用导数判断f(x)=2x+

在[

,+∞)上单调递增,在(0,

]上单调递减,从而可确定函数f(x)当x>0时的值域.
点评:本题考查函数奇偶性与单调性的综合,难点在于函数单调增区间的确定(导数法先判断,再用定义证明),着重考查函数奇偶性与单调性的性质及其应用,综合性强,属于难题.

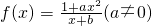 是奇函数,并且函数f(x)的图象经过点(1,3)
是奇函数,并且函数f(x)的图象经过点(1,3)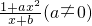 是奇函数,
是奇函数,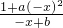 +
+ =(1+ax2)•
=(1+ax2)•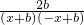 =0,
=0,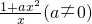 ,又f(x)的图象经过点(1,3),
,又f(x)的图象经过点(1,3),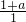 =3,
=3, ;
; 在[
在[ ,+∞)上单调递增.
,+∞)上单调递增. ≤x1<x2,
≤x1<x2, -
- )=(x2-x1)(2-
)=(x2-x1)(2-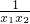 ),
), ≤x1<x2,
≤x1<x2,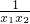 <2,于是2-
<2,于是2-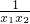 >0,
>0,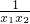 )>0,
)>0, 在[
在[ ,+∞)上单调递增.
,+∞)上单调递增. (x>0),
(x>0), ,由f′(x)≥0可得x≥
,由f′(x)≥0可得x≥ ,由f′(x)<0可得0<x<
,由f′(x)<0可得0<x< ,
, 在[
在[ ,+∞)上单调递增,在(0,
,+∞)上单调递增,在(0, ]上单调递减.
]上单调递减. 在x=
在x= 处取到最小值2
处取到最小值2 ,
, 的值域为:[2
的值域为:[2 ,+∞).
,+∞). 在[
在[ ,+∞)上单调递增,利用单调性的定义证明即可;
,+∞)上单调递增,利用单调性的定义证明即可; 在[
在[ ,+∞)上单调递增,在(0,
,+∞)上单调递增,在(0, ]上单调递减,从而可确定函数f(x)当x>0时的值域.
]上单调递减,从而可确定函数f(x)当x>0时的值域.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案 是奇函数,并且函数f(x)的图象经过点(1,3),
是奇函数,并且函数f(x)的图象经过点(1,3),