
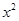 -6x+21)+f(
-6x+21)+f(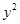 -8y)<0恒成立,则当x>3时,
-8y)<0恒成立,则当x>3时,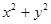 的取值范围是( )
的取值范围是( ) 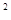 -6x+21)+f(y
-6x+21)+f(y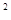 -8y)<0恒成立,可把问题转化为(x-3)
-8y)<0恒成立,可把问题转化为(x-3)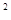 +(y-4)
+(y-4)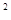 <4,借助于的有关知识可求.
<4,借助于的有关知识可求.
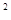 -6x+21)+f(y
-6x+21)+f(y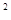 -8y)<0恒成立
-8y)<0恒成立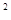 -6x+21)<-f(y
-6x+21)<-f(y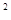 -8y)=f(8y-y
-8y)=f(8y-y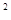 )恒成立,
)恒成立,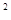 -6x+21<8y-y
-6x+21<8y-y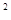 ,
,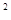 +(y-4)
+(y-4)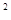 <4恒成立,
<4恒成立,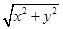 表示区域内的点和原点的距离.
表示区域内的点和原点的距离.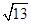 ,
,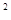 +y
+y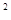 的范围为(13,49).
的范围为(13,49).

科目:高中数学 来源:不详 题型:单选题
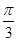 )的图象为C,则下列命题
)的图象为C,则下列命题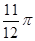 对称;
对称; 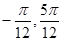 )内是增函数;
)内是增函数; 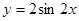 的图象向右平移
的图象向右平移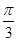 个单位长度可以得到图象C.
个单位长度可以得到图象C.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
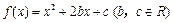 ,且
,且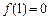 .
.
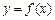 与x轴的两个交点
与x轴的两个交点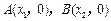 之间的距离为2,求b的值;
之间的距离为2,求b的值; 方程
方程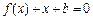 的两个实数根分别在区间
的两个实数根分别在区间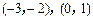 内,求b的取值范
内,求b的取值范 围.
围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 -f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=________.
-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com