
已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k为负数,且f (x)在区间[0,2]上有表达式f(x)=x(x-2).
(1)求f(-1),f(2.5)的值;
(2)写出f(x)在[-3,3]上的表达式,并讨论函数f(x)在[-3,3]上的单调性;
(3)求出f(x)在[-3,3]上的最小值与最大值,并求出相应的自变量的取值.
(1)f(-1)=-k f(2.5)=-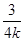
(2) f(x)= f(x)在[-3,-1]与[1,3]上为增函数,在[-1,1]上为减函数
f(x)在[-3,-1]与[1,3]上为增函数,在[-1,1]上为减函数
(3) ①k<-1时,f(x)在x=-3处取得最小值f(-3)=-k2,
在x=-1处取得最大值f(-1)=-k.
②k=-1时,f(x)在x=-3与x=1处取得最小值f(-3)=f(1)=-1,
在x=-1与x=3处取得最大值f(-1)=f(3)=1.
③-1<k<0时,f(x)在x=1处取得最小值f(1)=-1,在x=3处取得最大值f(3)=-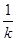 .
.
解析解:(1)f(-1)=kf(1)=-k,
∵f(0.5)=kf(2.5),
∴f(2.5)=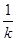 f(0.5)=
f(0.5)=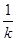 (0.5-2)×0.5=-
(0.5-2)×0.5=-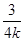 .
.
(2)∵对任意实数x,f(x)=kf(x+2),
∴f(x-2)=kf(x),
∴f(x)=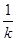 f(x-2),
f(x-2),
当-2≤x<0时,0≤x+2<2,f(x)=kf(x+2)=kx(x+2);
当-3≤x<-2时,-1≤x+2<0,
f(x)=kf(x+2)=k2(x+2)(x+4);
当2<x≤3时,0<x-2≤1,
f(x)=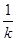 f(x-2)=
f(x-2)=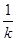 (x-2)(x-4).
(x-2)(x-4).
故f(x)=
∵k<0,
∴f(x)在[-3,-1]与[1,3]上为增函数,在[-1,1]上为减函数.
(3)由函数f(x)在[-3,3]上的单调性可知,
f(x)在x=-3或x=1处取得最小值f(-3)=-k2或f(1)=-1,
而在x=-1或x=3处取得最大值f(-1)=-k或f(3)=-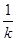 .
.
故有①k<-1时,f(x)在x=-3处取得最小值f(-3)=-k2,
在x=-1处取得最大值f(-1)=-k.
②k=-1时,f(x)在x=-3与x=1处取得最小值f(-3)=f(1)=-1,
在x=-1与x=3处取得最大值f(-1)=f(3)=1.
③-1<k<0时,f(x)在x=1处取得最小值f(1)=-1,在x=3处取得最大值f(3)=-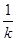 .
.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:解答题
据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本 (万元)可以看成月产量
(万元)可以看成月产量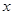 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本 (万元)关于月产量
(万元)关于月产量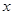 (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
修建一个面积为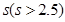 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米.已知后面墙的造价为每米45元,其他墙的造价为每米180元,设后面墙长度为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米.已知后面墙的造价为每米45元,其他墙的造价为每米180元,设后面墙长度为 米,修建此矩形场地围墙的总费用为
米,修建此矩形场地围墙的总费用为 元.
元.
(1)求 的表达式;
的表达式;
(2)试确定 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①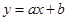 ;②
;②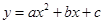 ;③
;③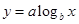 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=loga(3-ax).
(1)当x∈[0,2]时,函数f(x)恒有意义,求实数a的取值范围.
(2)是否存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1?如果存在,试求出a的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com