
辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①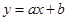 ;②
;②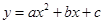 ;③
;③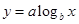 .
. 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
已知函数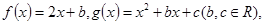 对任意的
对任意的 恒有
恒有 成立.
成立.
(1)当b=0时,记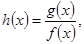 若
若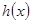 在
在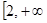 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围;
(2)证明:当 时,
时,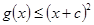 成立;
成立;
(3)若对满足条件的任意实数b,c,不等式 恒成立,求M的最小值.
恒成立,求M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k为负数,且f (x)在区间[0,2]上有表达式f(x)=x(x-2).
(1)求f(-1),f(2.5)的值;
(2)写出f(x)在[-3,3]上的表达式,并讨论函数f(x)在[-3,3]上的单调性;
(3)求出f(x)在[-3,3]上的最小值与最大值,并求出相应的自变量的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品x(百台),其总成本为g(x)万元(总成本=固定成本+生产成本),并且销售收人r(x)满足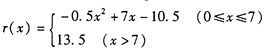
假定该产品产销平衡,根据上述统计规律求:
(1)要使工厂有盈利,产品数量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某物体的温度θ(单位:摄氏度)随时间t(单位:分钟)的变化规律是:θ=m·2t+21-t(t≥0,且m>0).
(1)如果m=2,求经过多少时间,物体的温度为5摄氏度.
(2)若物体的温度总不低于2摄氏度,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某化工企业2012年底投入100万元购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.设该企业使用该设备x年的年平均污水处理费用为y(单元:万元).
(1)用x表示y;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备.求该企业几年后需要重新更换新的污水处理设备.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设f(x)和g(x)都是定义在同一区间上的两个函数,若对任意x∈[1,2],都有|f(x)+g(x)|≤8,则称f(x)和g(x)是“友好函数”,设f(x)=ax,g(x)=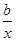 .
.
(1)若a∈{1,4},b∈{-1,1,4},求f(x)和g(x)是“友好函数”的概率;
(2)若a∈[1,4],b∈[1,4],求f(x)和g(x)是“友好函数”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com