
函数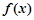 定义在区间
定义在区间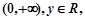 都有
都有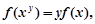 且
且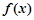 不恒为零.
不恒为零.
(1)求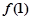 的值;
的值;
(2)若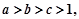 且
且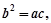 求证:
求证: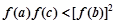 ;
;
(3)若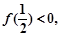 求证:
求证: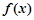 在
在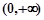 上是增函数.
上是增函数.
(1)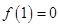 .(2)(3)见解析
.(2)(3)见解析
解析试题分析:(1)通过带特殊值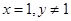 可求得;(2)设
可求得;(2)设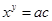 ,同取以
,同取以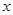 为底的对数得
为底的对数得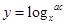 ,
,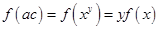 ,把
,把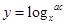 代入在运用对数运算性质就可得
代入在运用对数运算性质就可得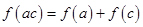 ,有
,有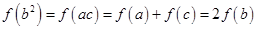 ,所以
,所以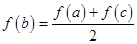 ,要证
,要证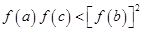 只需证
只需证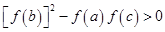 ,由以上很容易得到
,由以上很容易得到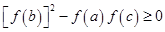 ,需要证出
,需要证出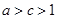 时,
时,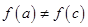 即等号不成立;(3)设
即等号不成立;(3)设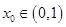 ,则
,则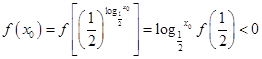 ,所以得
,所以得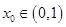 时,
时,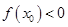 ,任取
,任取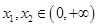 ,
,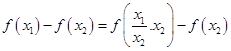 得证.
得证.
试题解析:⑴令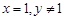 ,
,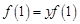 ,
,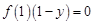 ,
,
因为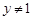 ,所以
,所以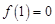 . 3分
. 3分
⑵设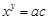 ,则
,则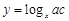 ,所以
,所以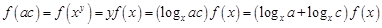
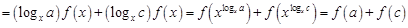 , 5分
, 5分
因为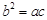 ,所以
,所以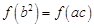 ,所以
,所以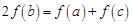 ,
,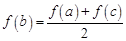 ,
,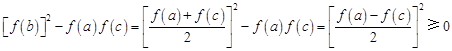 . 8分
. 8分
下面证明当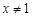 时,
时,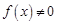 .
.
假设存在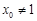 ,
,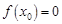 ,则对于任意
,则对于任意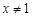 ,
,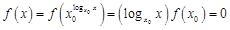 ,不合题意.所以,当
,不合题意.所以,当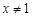 时,
时,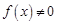 .
.
因为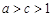 ,所以存在
,所以存在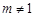 ,
, ,
,
所以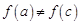 ,所以
,所以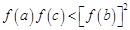 . 10分
. 10分
⑶设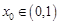 ,则
,则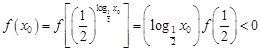 , 12分
, 12分
设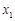 ,
, 为区间
为区间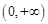 内的任意两个值,且
内的任意两个值,且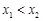 ,则
,则 ,由⑵的证明知,
,由⑵的证明知,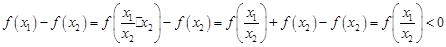 ,
,
所以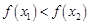 ,所以
,所以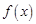 在
在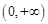 上是增函数. 16分
上是增函数. 16分
考点:1.函数附特殊值法;2.函数的构造法;3.证明单调函数.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①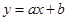 ;②
;②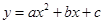 ;③
;③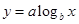 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).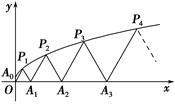
(1)写出a1,a2,a3;
(2)求出点An(an,0)(n∈N*)的横坐标an关于n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为 米,圆心角为
米,圆心角为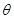 (弧度).
(弧度).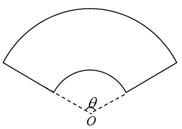
(1)求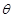 关于
关于 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 为何值时,
为何值时, 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点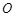 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点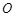 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为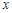 米,圆心角为
米,圆心角为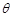 (弧度).
(弧度).
(1)求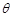 关于
关于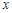 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为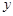 ,求
,求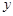 关于
关于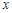 的函数关系式,并求出
的函数关系式,并求出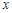 为何值时,
为何值时,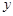 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N).前30天价格为g(t)=t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系;
(2)求日销售额S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com