
设函数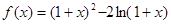
(1)若关于x的不等式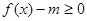 在
在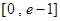 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设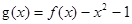 ,若关于x的方程
,若关于x的方程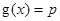 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.
(3)证明不等式: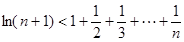
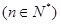
(1)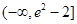 (2)p的最小值为0
(2)p的最小值为0
解析试题分析:
(1)存在性问题,只需要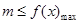 即可,再利用导数法求解f(x)的最大值(即求导,求单调性,求极值9与端点值比较得出最值).
即可,再利用导数法求解f(x)的最大值(即求导,求单调性,求极值9与端点值比较得出最值).
(2)p的最小值为函数g(x)的最小值,利用导数求函数的最小值即可(即求导,求单调性,求极值9与端点值比较得出最值).
(3)利用第二问结果可以得到与不等式有关的恒等式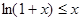 .令
.令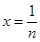 .把n=1,2,3,,得n个不等式左右相加,左边利用对数除法公式展开即可用裂项求和法得到不等式的左边,即证得原式
.把n=1,2,3,,得n个不等式左右相加,左边利用对数除法公式展开即可用裂项求和法得到不等式的左边,即证得原式
试题解析:
(1)依题意得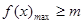
 ,而函数
,而函数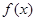 的定义域为
的定义域为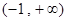
∴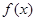 在
在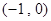 上为减函数,在
上为减函数,在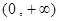 上为增函数,则
上为增函数,则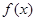 在
在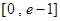 上为增函数
上为增函数
,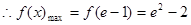 即实数m的取值范围为
即实数m的取值范围为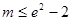 4分
4分
(2)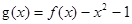
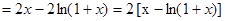 则
则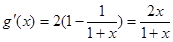
显然,函数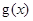 在
在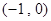 上为减函数,在
上为减函数,在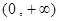 上为增函数,则函数
上为增函数,则函数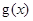 的最小值为
的最小值为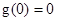
所以,要使方程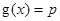 至少有一个解,则
至少有一个解,则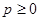 ,即p的最小值为0 8分
,即p的最小值为0 8分
(3)由(2)可知:  在
在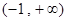 上恒成立
上恒成立
所以 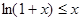 ,当且仅当x=0时等号成立
,当且仅当x=0时等号成立
令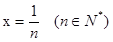 ,则
,则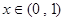 代入上面不等式得:
代入上面不等式得: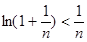
即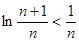 , 即
, 即 
所以,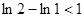 ,
,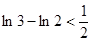 ,
,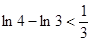 ,,
,,
将以上n个等式相加即可得到: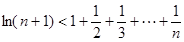 12分
12分
考点:导数 不等式 函数最值


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点对称的点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的定义域为
的定义域为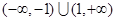 ,对定义域内的任意x,满足
,对定义域内的任意x,满足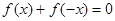 ,当
,当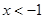 时,
时,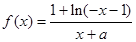 (a为常),且
(a为常),且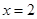 是函数
是函数 的一个极值点,
的一个极值点,
(1)求实数a的值;
(2)如果当 时,不等式
时,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(3)求证: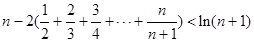
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 两城相距
两城相距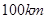 ,在两地之间距
,在两地之间距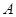 城
城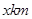 处
处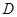 地建一核电站给
地建一核电站给 两城供电.为保证城市安全,核电站距城市距离不得少于
两城供电.为保证城市安全,核电站距城市距离不得少于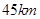 .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离(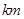 )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数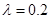 ,若
,若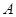 城供电量为
城供电量为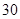 亿度/月,
亿度/月,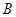 城为
城为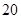 亿度/月.
亿度/月.
(Ⅰ)把月供电总费用 表示成
表示成 的函数,并求定义域;
的函数,并求定义域;
(Ⅱ)核电站建在距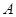 城多远,才能使供电费用最小,最小费用是多少?
城多远,才能使供电费用最小,最小费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
(1)如果瓶内的药液恰好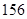 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后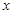 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为 (单位:厘米),已知当
(单位:厘米),已知当 时,
时,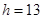 .试将
.试将 表示为
表示为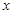 的函数.(注:
的函数.(注: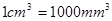 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设f(x)和g(x)都是定义在同一区间上的两个函数,若对任意x∈[1,2],都有|f(x)+g(x)|≤8,则称f(x)和g(x)是“友好函数”,设f(x)=ax,g(x)=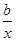 .
.
(1)若a∈{1,4},b∈{-1,1,4},求f(x)和g(x)是“友好函数”的概率;
(2)若a∈[1,4],b∈[1,4],求f(x)和g(x)是“友好函数”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com