
某化工企业2012年底投入100万元购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.设该企业使用该设备x年的年平均污水处理费用为y(单元:万元).
(1)用x表示y;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备.求该企业几年后需要重新更换新的污水处理设备.
科目:高中数学 来源: 题型:解答题
辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①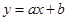 ;②
;②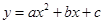 ;③
;③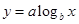 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=loga(3-ax).
(1)当x∈[0,2]时,函数f(x)恒有意义,求实数a的取值范围.
(2)是否存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1?如果存在,试求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2|x-2|+ax(x∈R)有最小值.
(1)求实数a的取值范围.
(2)设g(x)为定义在R上的奇函数,且当x<0时,g(x)=f(x),求g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).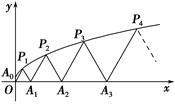
(1)写出a1,a2,a3;
(2)求出点An(an,0)(n∈N*)的横坐标an关于n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点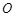 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点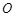 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为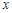 米,圆心角为
米,圆心角为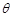 (弧度).
(弧度).
(1)求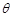 关于
关于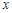 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为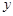 ,求
,求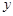 关于
关于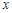 的函数关系式,并求出
的函数关系式,并求出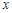 为何值时,
为何值时,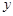 取得最大值?
取得最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com