
如果a,b,c都是实数,那么P:ac<0,是q:关于x的方程ax2+bx+c=0有一个正根和一个负根的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:单选题
已知下列命题中:
(1)若 ,且
,且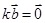 ,则
,则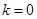 或
或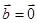 ,
,
(2)若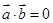 ,则
,则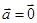 或
或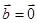
(3)若不平行的两个非零向量 ,满足
,满足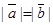 ,则
,则
(4)若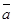 与
与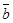 平行,则
平行,则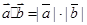 其中真命题的个数是( )
其中真命题的个数是( )
A. | B.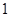 | C. | D.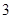 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
给出以下四个说法:
①p或q为真命题是p且q为真命题的充分不必要条件;
②在刻画回归模型的拟合效果时,相关指数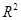 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程 中,当解释变量
中,当解释变量 每增加一个单位时,预报变量
每增加一个单位时,预报变量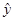 平均增加
平均增加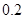 个单位;
个单位;
④对分类变量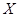 与
与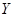 ,若它们的随机变量
,若它们的随机变量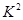 的观测值
的观测值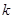 越小,则判断“
越小,则判断“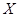 与
与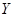 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是 ( )
| A.①④ | B.②④ | C.①③ | D.②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
由命题“存在x∈R,使e|x-1|-m≤0”是假命题,得m的取值范围是(-∞,a),则实数a的取值是( )
| A.(-∞,1) | B.(-∞,2) | C.1 | D.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列命题中真命题是( )
①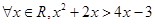
②命题“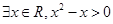 ”的否定是“
”的否定是“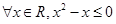 ”
”
③“若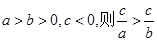 ”的逆否命题是真命题
”的逆否命题是真命题
④若命题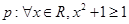 。命题
。命题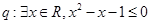 。
。
则命题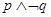 是真命题。
是真命题。
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com