[题目]如图.已知抛物线的焦点为.直线过且依次交抛物线及圆于点四点.则的最小值为( )A. B. C. D. 题目和参考答案——青夏教育精英家教网—

【题目】如图，已知抛物线的焦点为，直线过且依次交抛物线及圆于点四点，则的最小值为（）

A. B. C. D.

【答案】B

【解析】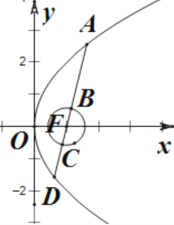

如图所示，抛物线的焦点，圆的圆心坐标是，半径，设，由抛物线的定义可知，，显然直线不可能平行于轴，设直线的方程为代入到抛物线的方程中，得，，显然，，等号成立当且仅当和同时成立，即等号成立当且仅当，的最小值是，故选B.

【方法点睛】本题主要考查抛物线的定义和几何性质，以及基本不等式求最值，属于难题. 与焦点、准线有关的问题一般情况下都与拋物线的定义有关，解决这类问题一定要注意点到点的距离与点到直线的距离的转化：（1）将抛线上的点到准线距转化为该点到焦点的距离；(2)将抛物线上的点到焦点的距离转化为到准线的距离，本题就是将转化为到准线的距离后，再利用韦达定理与基本不等式使问题得到解决的.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设函数f（x）=x|x|+bx+c（b，c∈R），给出如下四个命题：①若c=0，则f（x）为奇函数；②若b=0，则函数f（x）在R上是增函数；③函数y=f（x）的图象关于点（0，c）成中心对称图形；④关于x的方程f（x）=0最多有两个实根．其中正确的命题

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】四名同学根据各自的样本数据研究变量之间的相关关系，并求得回归直线方程，分别得到以下四个结论：(　　)

①与负相关且. ②与负相关且

③与正相关且 ④与正相关且

其中正确的结论的序号是（）

A. ①② B. ②③ C. ①④ D. ③④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

(Ⅰ)若为函数的极值点,求的值；

(Ⅱ)讨论在定义域上的单调性.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知为坐标原点，是椭圆上的点，设动点满足.

（1）求动点的轨迹的方程；

（2）若直线与曲线相交于，两个不同点，求面积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】轮船从某港口将一些物品送到正航行的轮船上，在轮船出发时，轮船位于港口北偏西且与相距20海里的处，并正以30海里的航速沿正东方向匀速行驶，假设轮船沿直线方向以海里/小时的航速匀速行驶，经过小时与轮船相遇.

（1）若使相遇时轮船航距最短，则轮船的航行速度大小应为多少？

（2）假设轮船的最高航速只能达到30海里/小时，则轮船以多大速度及什么航行方向才能在最短时间与轮船相遇，并说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本题满分12分）为选拔选手参加“中国汉字听写大会”，某中学举行了一次“汉字听写大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为）进行统计．按照，，，，的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在，的数据）．