
【题目】在如图所示的几何体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 到平面
到平面![]() 的距离;
的距离;
(3)求三棱锥![]() 的体积.
的体积.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)先根据面面垂直性质定理得![]() 平面
平面![]() ,即得
,即得![]() ,再利用勾股定理得
,再利用勾股定理得![]() ,最后根据线面垂直判定定理得结论(2)先根据平行转化
,最后根据线面垂直判定定理得结论(2)先根据平行转化![]() 到平面
到平面![]() 的距离为点
的距离为点![]() 到平面
到平面![]() 的距离,再作
的距离,再作![]() ,由面面垂直性质定理得
,由面面垂直性质定理得![]() 平面
平面![]() ,最后计算
,最后计算![]() 即得结果(3)由于已知
即得结果(3)由于已知![]() 到平面
到平面![]() 的距离,所以利用等体积法先转化为
的距离,所以利用等体积法先转化为![]() ,再根据锥体体积公式求体积
,再根据锥体体积公式求体积
试题解析:(1)∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
∵![]() ,∴
,∴![]() .
.
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,
, ![]() 平面
平面![]() ,
,
所以点![]() 到平面
到平面![]() 的距离就等于点
的距离就等于点![]() 到平面
到平面![]() 的距离,
的距离,
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
(3)∴![]() ,
,
∵![]() ,
,
∴![]() ,即三棱锥
,即三棱锥![]() 的体积为
的体积为![]() .
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
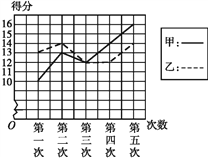
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法: ①分类变量A与B的随机变量K2越大,说明“A与B有关系”的可信度越大.
②以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=lny,将其变换后得到线性方程z=0.3x+4,则c,k的值分别是e4和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为y=a+bx中,b=1, ![]() =1,
=1, ![]() =3,
=3,
则a=1.正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
反感 | 10 | ||
不反感 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是 ![]() .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
提示:可参考试卷第一页的公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是某池塘中的浮萍蔓延的面积![]() 与时间
与时间![]() 月)的关系
月)的关系![]() 有以下叙述:
有以下叙述:
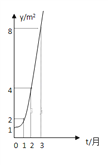
①这个指数函数的底数是2;
②第5个月时,浮萍的面积就会超过![]()
③浮萍从![]() 蔓延到
蔓延到![]() 需要经过1.5个月;
需要经过1.5个月;
④浮萍每个月增加的面积都相等;
⑤若浮萍蔓延到![]() 所经过的时间分别为
所经过的时间分别为![]() 则
则![]() .其中正确的是
.其中正确的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,记
,记![]()
![]() .
.
(Ⅰ)求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() ,求
,求 ![]() 的值;
的值;
(Ⅲ)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象,若函数
的图象,若函数![]() 在
在![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆AOB是某市休闲广场的平面示意图,半径OA的长为10,管理部门在A,B两处各安装好一个光源,其相应的光强度分别为4和9,根据光学原理,地面上某处照度y与光强度I成正比,与光源距离x的平方成反比,即y= ![]() (k为比例系数),经测量,在弧AB的中心C处的照度为130.(C处的照度为A,B两处光源的照度之和)
(k为比例系数),经测量,在弧AB的中心C处的照度为130.(C处的照度为A,B两处光源的照度之和) 
(1)求比例系数k的值;
(2)现在管理部门计划在半圆弧AB上,照度最小处增设一个光源P,试问新增光源P安装在什么位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com