
函数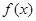 在
在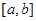 上有定义,若对任意
上有定义,若对任意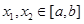 ,有
,有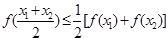
则称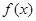 在
在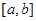 上具有性质
上具有性质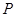 .设
.设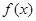 在[1,3]上具有性质
在[1,3]上具有性质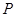 ,现给出如下题:①
,现给出如下题:①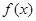 在
在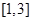 上的图像时连续不断的; ②
上的图像时连续不断的; ②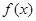 在
在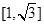 上具有性质
上具有性质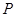 ;
;
③若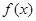 在
在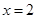 处取得最大值
处取得最大值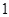 ,则
,则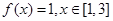 ;④对任意
;④对任意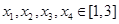 ,有
,有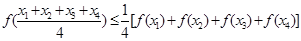
其中真命题的序号( )
A.①② B.①③ C.②④ D.②③④
科目:高中数学 来源: 题型:
| F(u)-F(v) | u-v |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 3 |
| x1+x2+x3+x4 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| 1 |
| f(x) |
| x1+x2+x3+x4 |
| 4 |
| f(x1)+f(x2)+f(x3)+f(x4) |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| v2-u2 |
| v-u |
| F(u)-F(v) |
| u-v |
| 1 | ||
2
|
| x |
查看答案和解析>>
科目:高中数学 来源:2010年福建省八县(市高二下学期期末联考(文科)数学卷 题型:填空题
设函数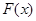 和
和 都在区间
都在区间 上有定义,若对
上有定义,若对 的任意子区间
的任意子区间 ,总有
,总有 上的实数
上的实数 和
和 ,使得不等式
,使得不等式 成立,则称
成立,则称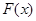 是
是 在区间
在区间 上的甲函数,
上的甲函数, 是
是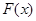 在区间
在区间 上的乙函数.已知
上的乙函数.已知 ,那么
,那么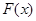 的乙函数
的乙函数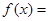 _____________
_____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com