Question

已知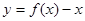恰有3个不同的零点，则实数的取值范围是  （   ）

A．

B．

C．

D．

Answer 1

A

解析试题分析：对于函数，
因为当x≥0的时候，f（x）=f（x－1），所以所有大于等于0的x代入得到的f（x）相当于在[－1，0）重复的周期函数，
x∈[－1，0）时，y=a－x²－2x=1+a－（x+1）²，对称轴x=－1，顶点（－1，1+a）。
（1）如果a＜－1，函数y=f（x）－x至多有2个不同的零点；
（2）如果a=－1，则y有一个零点在区间（－1，0），有一个零点在（－∞，－1），一个零点是原点；
（3）如果a＞－1，则有一个零点在（－∞，－1），y右边有两个零点，
故实数a的取值范围是[－1，+∞），
故选A．
考点：分段函数的概念，函数的周期性、对称性，函数的零点。
点评：中档题，认识构成的特殊性，将问题的研究转化成周期函数图象的研究，通过考察二次函数图象，讨论a的不同取值范围时，函数零点的情况，达到解题目的。