（本题满分20分）
设
是定义在实数
上的函数，
是定义在正整数
上的函数，同时满足下列条件：
（1）任意
，有
，当
时，
且
；
（2）
；
（3）
，
试求：（1）证明：任意， 
，都有
；
（2）是否存在正整数
，使得
是25的倍数，若存在，求出所有自然数；若不存在说明理由． （阶乘定义：
）
天天练口算系列答案科目：高中数学 来源：2014届江苏省高二上学期期中考试数学试卷（解析版） 题型：解答题
（本题满分20分）设直线l1：y＝k1x＋1，l2：y＝k2x－1，其中实数k1，k2满足k1k2＋1＝0.
（Ⅰ）证明：直线l1与l2相交；（Ⅱ）试用解析几何的方法证明：直线l1与l2的交点到原点距离为定值．（Ⅲ）设原点到l1与l2的距离分别为d1和d2求d1+d2的最大值
查看答案和解析>>
科目：高中数学 来源： 题型：
（本题满分20分，其中第1小题4分，第2小题6分，第3小题10分）
已知
是直线
上的
个不同的点（
，
、
均为非零常数），其中数列
为等差数列.
（1）求证：数列
是等差数列；
（2）若点
是直线
上一点，且
，求证: 
；
（3） 设
，且当
时，恒有
（
和
都是不大于的正整数, 且
）.试探索：在直线上是否存在这样的点，使得
成立？请说明你的理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
（本题满分20分，其中第1小题4分，第2小题6分，第3小题10分.）
平面直角坐标系
中，已知
，…，
是直线
上的
个点（
，
、
均为非零常数）.
（1）若数列
成等差数列，求证：数列
也成等差数列；
（2）若点
是直线
上一点，且
，求
的值；
（3）若点满足
，我们称
是向量
，
，…，
的线性组合,
是该线性组合的系数数列.
当是向量，，…，的线性组合时，请参考以下线索：
① 系数数列需满足怎样的条件，点会落在直线上？
② 若点落在直线上，系数数列会满足怎样的结论？
③ 能否根据你给出的系数数列满足的条件，确定在直线上的点的个数或坐标？
试提出一个相关命题（或猜想）并开展研究，写出你的研究过程.【本小题将根据你提出的命题（或猜想）的完备程度和研究过程中体现的思维层次，给予不同的评分】
查看答案和解析>>
科目：高中数学 来源：2010年陕西省西安市铁一中高二下学期期中考试数学（文） 题型：解答题
(附加题)本题满分20分
如图，已知抛物线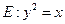
与圆
相交于A、B、C、D四个点。
（Ⅰ）求r的取值范围 （Ⅱ）当四边形ABCD的面积最大时，求对角线AC、BD的交点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
时，
， 
，
，则得
，不可能，舍去 
时，
，得，
，则，
，
，
，
，
任意
， 
，都有
为单调减函数
…①
，
，
，
，
，
，
，
，
，
，
时，
能被25整除
，当
或
时，
是25的倍数
