
分析 利用平面向量的三角形法则,将$\overrightarrow{BP}$,$\overrightarrow{CQ}$分别AP,AC,AB对应的向量表示,进行数量积的运算,得到关于$\overrightarrow{AP},\overrightarrow{CB}$夹角θ的余弦函数解析式,借助于有界性求最值即可.
解答 解: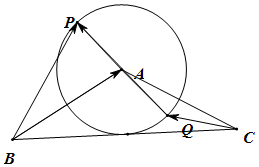 如图:由已知$\overrightarrow{BP}•\overrightarrow{CQ}=({\overrightarrow{BA}+\overrightarrow{AP}})•({\overrightarrow{CA}-\overrightarrow{AP}})=\overrightarrow{BA}•\overrightarrow{CA}+\overrightarrow{AP}•({\overrightarrow{CA}-\overrightarrow{BA}})-{\overrightarrow{AP}^2}$
如图:由已知$\overrightarrow{BP}•\overrightarrow{CQ}=({\overrightarrow{BA}+\overrightarrow{AP}})•({\overrightarrow{CA}-\overrightarrow{AP}})=\overrightarrow{BA}•\overrightarrow{CA}+\overrightarrow{AP}•({\overrightarrow{CA}-\overrightarrow{BA}})-{\overrightarrow{AP}^2}$
=$2×2×(-\frac{1}{2})+\overrightarrow{AP}•\overrightarrow{CB}-1$
=$-2+2\sqrt{3}cosθ-1≤2\sqrt{3}-3$;
故答案为:$2\sqrt{3}-3$.
点评 本题考查了平面向量的数量积运算,借助于余弦函数的有界性求最值;属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {an}为首项为正项的等比数列,若a2n-1+a2n<0,则公比q<0 | |
| B. | 若{an}为递增数列,则an+1>|an| | |
| C. | {an}为等差数列,若Sn+1>Sn,则{an}单调递增 | |
| D. | {an}为等差数列,若{an}单调递增,则Sn+1>Sn. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com