
科目:高中数学 来源:2016届浙江稽阳联谊学校高三4月联考数学(文)试卷(解析版) 题型:解答题
已知等比数列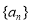 的前
的前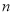 项和为
项和为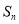 ,
,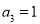 且
且 为等差数列
为等差数列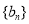 的前三项.
的前三项.
(1)求 与数列
与数列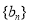 的通项公式;
的通项公式;
(2)设数列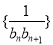 的前
的前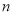 项和
项和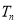 ,试问是否存在正整数
,试问是否存在正整数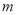 ,对任意的
,对任意的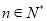 使得
使得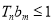 ?若存在请求出
?若存在请求出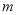 的最大值,若不存在请说明理由.
的最大值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源:2017届山东省高三第一次诊断数学(理)试卷(解析版) 题型:解答题
在研究塞卡病毒(Zika virus)某种疫苗的过程中,为了研究小白鼠连续接种该种疫苗后出现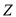 症状的情况,做接种试验,试验设计每天接种一次,连续接种3天为一个接种周期.已知小白鼠接种后当天出现
症状的情况,做接种试验,试验设计每天接种一次,连续接种3天为一个接种周期.已知小白鼠接种后当天出现 症状的概率为
症状的概率为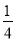 ,假设每次接种后当天是否出现
,假设每次接种后当天是否出现 症状与上次接种无关.
症状与上次接种无关.
(1)若出现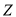 症状即停止试验,求试验至多持续一个接种周期的概率;
症状即停止试验,求试验至多持续一个接种周期的概率;
(2)若在一个接种周期内出现2次货3次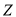 症状,则这个接种周期结束后终止试验,试验至多持续3个周期,设接种试验持续的接种周期数为
症状,则这个接种周期结束后终止试验,试验至多持续3个周期,设接种试验持续的接种周期数为 ,求
,求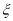 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2017届山东省高三第一次诊断数学(理)试卷(解析版) 题型:选择题
已知定义在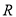 上的偶函数
上的偶函数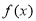 满足
满足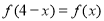 ,且
,且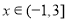 时,
时, 则
则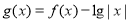 的零点个数是( )
的零点个数是( )
A.9 B.10 C.18 D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com