
(12分)已知 是函数
是函数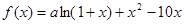 的一个极值点。
的一个极值点。
(1)求 ; (2)求函数
; (2)求函数 的单调区间;
的单调区间;
(3)若直线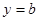 与函数
与函数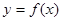 的图象有3个交点,求
的图象有3个交点,求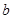 的取值范围。
的取值范围。
(Ⅰ)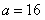 .(Ⅱ)
.(Ⅱ)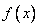 的单调增区间是
的单调增区间是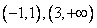 ,
,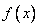 的单调减区间是
的单调减区间是 .(Ⅲ)
.(Ⅲ)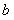 的取值范围为
的取值范围为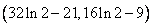 。
。
【解析】本试题主要是考察了导数在研究函数的中 运用,利用函数的极值点可知导数为零得到参数的取值,然后求解析式,并利用导数来判定函数的单调性以及研究常函数与函数的交点的问题的综合运用。
(1)利用函数在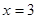 是函数
是函数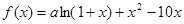 的一个极值点,说明了该点的导数值为零,得到参数的值。
的一个极值点,说明了该点的导数值为零,得到参数的值。
(2)利用第一问的结论求解导数,判定单调区间。
(3)要研究常函数与已知函数的交点问题,关键是弄清楚,函数y=f(x)与坐标轴的位置关系即可。
解:(Ⅰ)因为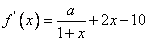 ,所以
,所以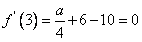 ,因此
,因此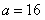 .
.
(Ⅱ)由(Ⅰ)知,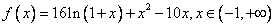 ,
,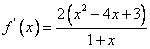 ,
,
当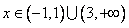 时,
时,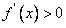 ,当
,当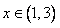 时,
时,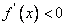 ,所以
,所以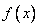 的单调增区间是
的单调增区间是
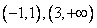 ,
,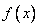 的单调减区间是
的单调减区间是 .
.
(Ⅲ)由(Ⅱ)知,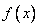 在
在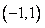 内单调增加,在
内单调增加,在 内单调减少,在
内单调减少,在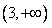 上单调增加,且当
上单调增加,且当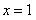 或
或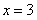 时,
时,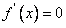 ,所以
,所以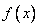 的极大值为
的极大值为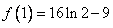 ,极小值为
,极小值为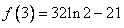 ,
,
因此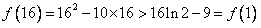 ,
,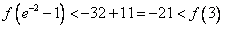 ,
,
所以在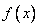 的三个单调区间
的三个单调区间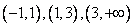 直线
直线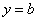 有
有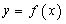 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当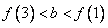 ,因此,
,因此,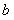 的取值范围为
的取值范围为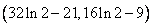 。
。


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2014届四川达州第一中学高二下学期第一次月考文科数学试卷(解析版) 题型:解答题
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中
(1)求 与
与 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)设函数函数g(x)= 
 ;试比较g(x)与
;试比较g(x)与 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东师大附中高三12月(第三次)模拟检测理科数学试卷(解析版) 题型:解答题
(本题满分12分)已知 是函数
是函数 的一个极值点.
的一个极值点.
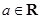

(Ⅰ)求 的值;
的值;
(Ⅱ)当 ,
, 时,证明:
时,证明:
查看答案和解析>>
科目:高中数学 来源:2013届浙江省宁波万里国际学校高二下期中文科数学试卷(解析版) 题型:解答题
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
,
(1)求 与
与 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)当 时,函数
时,函数 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省高三上学期第三次月考数学文卷 题型:解答题
(本小题满分15分)
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中
 。
。
(Ⅰ)求 与
与 的关系表达式;
的关系表达式;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)当 时,函数
时,函数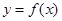 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求实数
,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二下学期第一次月考理科数学试卷 题型:解答题
(本小题满分14分)
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
,
(1)求 与
与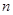 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)当 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com