练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    抛物线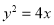的焦点到双曲线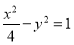的渐近线的距离是 ．

     

    【解析】

    试题分析：已知抛物线的焦点为，双曲线的渐近线方程为，所求距离为.

    考点：抛物线的焦点坐标，双曲线的渐近线，点到直线的距离.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年江苏省淮安市高三5月信息卷文科数学试卷（解析版） 题型：填空题

    已知数列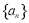是各项均不为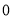的等差数列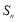，为其前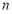项和，且满足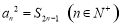．若不等式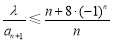对任意的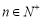恒成立，则实数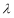的最大值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二文科数学试卷（解析版） 题型：填空题

    若关于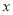的不等式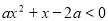的解集中有且仅有4个整数解，则实数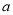的取值范围是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测三数学试卷（解析版） 题型：解答题

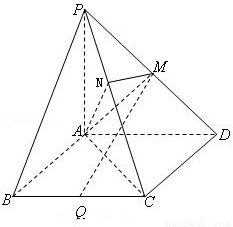
    如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，四边形ABCD是平行四边形，且AC⊥CD，PA=AD，M，Q分别是PD，BC的中点．

    （1）求证：MQ∥平面PAB；

    （2）若AN⊥PC，垂足为N，求证：MN⊥PD．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测三数学试卷（解析版） 题型：填空题

    已知不等式组表示的平面区域的面积为，若点，则的最大值为　　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江苏省高三下学期4月周练理科数学试卷（解析版） 题型：解答题

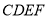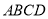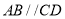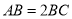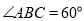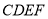
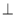    如图所示的几何体中，面为正方形，面为等腰梯形， ，，，且平面平面．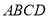

    (1)求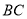与平面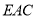所成角的正弦值；

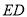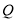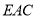
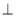    (2)线段上是否存在点，使平面平面？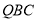

    证明你的结论．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江苏省高三下学期4月周练理科数学试卷（解析版） 题型：解答题

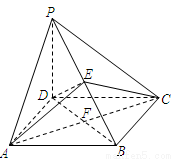
    如图，在四棱锥P－ABCD中，PD⊥平面ABCD，四边形ABCD是菱形，AC＝6，BD＝8，E是PB上任意一点，△AEC面积的最小值是3．

    （1）求证：AC⊥DE；

    （2）求四棱锥P－ABCD的体积．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江苏省高三下学期4月周练文科数学试卷（解析版） 题型：解答题

    一个如图所示的不规则形铁片，其缺口边界是口宽4分米，深2分米（顶点至两端点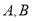所在直线的距离）的抛物线形的一部分，现要将其缺口边界裁剪为等腰梯形．

    （1）若保持其缺口宽度不变，求裁剪后梯形缺口面积的最小值；

    （2）若保持其缺口深度不变，求裁剪后梯形缺口面积的最小值．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江苏省徐州市高三第三次质量检测理科数学试卷（解析版） 题型：填空题

    已知复数（是虚数单位），则的虚部是 ．

     

    查看答案和解析>>

    同步练习册答案