
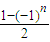 (n∈N*),我们可以发现f(n)有许多性质,如:f(2k)=0(k∈N*)等,下列关于f(n)的性质中一定成立的是( )
(n∈N*),我们可以发现f(n)有许多性质,如:f(2k)=0(k∈N*)等,下列关于f(n)的性质中一定成立的是( )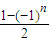 的函数值为:1,0,1,0,…,然后对选项进行判断,即可得出结论.
的函数值为:1,0,1,0,…,然后对选项进行判断,即可得出结论.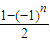 的函数值为:1,0,1,0,…
的函数值为:1,0,1,0,…

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-(-1)n |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:衢州一模 题型:单选题
| 1-(-1)n |
| 2 |
| A.f(n+1)-f(n)=1 | B.f(n+k)=f(n)(k∈N*) |
| C.αf(n)=f(n+1)+αf(n)(α≠0) | D.αf(n+1)=α-(α+1)f(n)(α≠0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com