
已知函数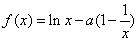 ,
,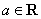 .
.
(1)求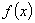 的单调区间;
的单调区间;
(2)若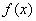 的最小值为0,回答下列问题:
的最小值为0,回答下列问题:
(ⅰ)求实数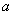 的值;
的值;
|
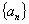 满足
满足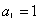 ,
,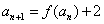 ,记[
,记[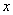 ]表示不大于
]表示不大于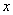 的最大整数,求
的最大整数,求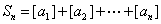 ,求
,求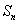 .
. 解:(1)函数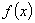 的定义域为
的定义域为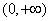 ,且
,且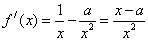 .
.
当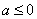 时,
时,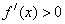 ,所以
,所以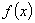 在区间
在区间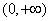 内单调递增;
内单调递增;
当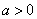 时,由
时,由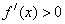 ,解得
,解得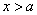 ;由
;由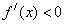 ,解得
,解得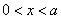 .
.
所以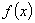 的单调递增区间为
的单调递增区间为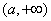 ,单调递减区间为
,单调递减区间为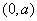 .
.
综上述: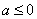 时,
时,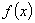 的单调递增区间是
的单调递增区间是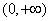 ;
;
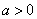 时,
时,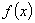 的单调递减区间是
的单调递减区间是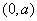 ,单调递增区间是
,单调递增区间是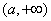 .
.
(2)(ⅰ)由(1)知,当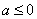 时,
时,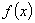 无最小值,不合题意;
无最小值,不合题意;
当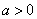 时,
时,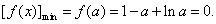
令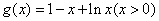 ,则
,则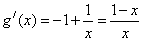 ,
,
由 ,解得
,解得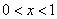 ;由
;由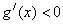 ,解得
,解得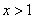 .
.
所以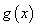 的单调递增区间为
的单调递增区间为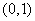 ,单调递减区间为
,单调递减区间为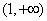 .
.
故 ,即当且仅当x=1时,
,即当且仅当x=1时,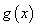 =0.
=0.
因此, .
.
(ⅱ)因为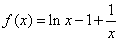 ,所以
,所以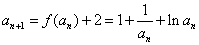 .
.
由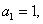 得
得 于是
于是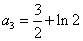 .因为
.因为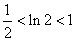 ,所以
,所以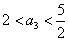 .
.
猜想当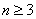 ,
, 时,
时, .
.
下面用数学归纳法进行证明.
①当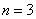 时,
时,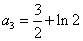 ,故
,故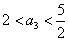 成立.
成立.
②假设当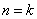 (
(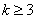 ,
,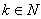 )时,不等式
)时,不等式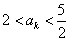 成立. 则当
成立. 则当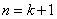 时,
时,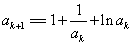 ,
,
 由(1)知函数
由(1)知函数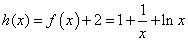 在区间
在区间 单调递增,
单调递增,
所以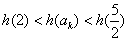 ,又因为
,又因为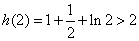 ,
,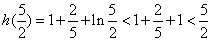 .
.
故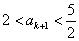 成立,即当
成立,即当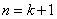 时,不等式成立.
时,不等式成立.
根据①②可知,当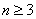 ,
, 时,不等式
时,不等式 成立.
成立.
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
如果对任意一个三角形,只要它的三边长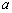 ,
,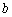 ,
,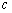 都在函数
都在函数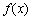 的定义域内,就有
的定义域内,就有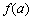 ,
,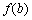 ,
,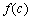 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称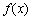 为“Л型函数”.则下列函数:
为“Л型函数”.则下列函数:
①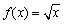 ; ②
; ②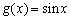
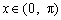 ; ③
; ③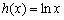
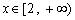 ,
,
是“Л型函数”的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数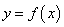 在区间
在区间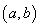 上的导函数为
上的导函数为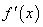 ,
,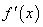 在区间
在区间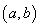 上的导函数为
上的导函数为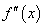 ,若在区间
,若在区间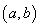 上
上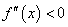 恒成立,则称函数
恒成立,则称函数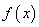 在区间
在区间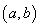 上为“凸函数” .已知
上为“凸函数” .已知 ,若对任意满足
,若对任意满足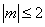 的实数
的实数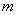 ,函数
,函数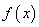 在区间
在区间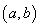 上为“凸函数”,则
上为“凸函数”,则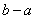 的最大值为
的最大值为
A.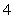 B.
B. C.
C.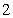 D.
D.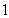
查看答案和解析>>
科目:高中数学 来源: 题型:
《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为( )
A.1升 B.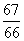 升 C.
升 C.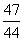 升 D.
升 D.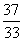 升
升
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com