
(本小题共12分)
在直角坐标系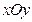 中,动点P到两定点
中,动点P到两定点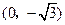 ,
,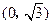 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为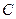 ,过点
,过点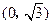 的直线与
的直线与 交于A,B两点.
交于A,B两点.
(1)写出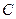 的方程;
的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值;若存在,求出d的最大值、最小值.
科目:高中数学 来源: 题型:
(本小题共12分) 在平面直角坐标系中,已知An(n,an)、Bn(n,bn)、Cn(n-1,0)(n∈N*),满足向量![]() 与向量
与向量![]() 共线,且点An(n,an) (n∈N*)都在斜率为2的同一条直线l上. 若
共线,且点An(n,an) (n∈N*)都在斜率为2的同一条直线l上. 若![]() a1=-3,b1=10
a1=-3,b1=10![]() (1)求数列{an}与{ bn }的通项公式;
(1)求数列{an}与{ bn }的通项公式;
(2)求当n取何值时△AnBnCn的面积Sn最小,并求出Sn的这个最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共12分)
在直角坐标系![]() 中,动点P到两定点
中,动点P到两定点![]() ,
,![]() 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为![]() ,过点
,过点![]() 的直线与
的直线与![]() 交于A,B两点.
交于A,B两点.
(1)写出![]() 的方程;
的方程;
(2)设d为A、B两点间的距离,d是否存在最大值、最小值;若存在, 求出d的最大值、最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测(三)文数学卷(解析版) 题型:解答题
(本小题共12分)
在如图的多面体中,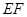 ⊥平面
⊥平面 ,
, ,
,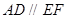 ,
,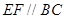 ,
,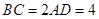 ,
,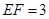 ,
,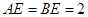 ,
, 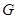 是
是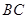 的中点.
的中点.
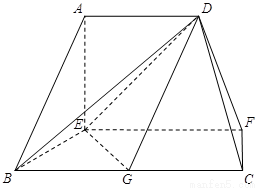
(Ⅰ)求证: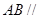 平面
平面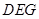 ;
;
(Ⅱ)求证: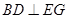 ;
;
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三普通高考考生知识能力水平摸底考试数学理卷 题型:解答题
(本小题共12分)
在直三棱柱ABC—A1B1C1中,AA1=1,AB=2,AC=1,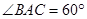 ,D为BC的中点。
,D为BC的中点。
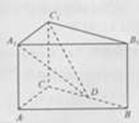
(I)求证:平面ACC1A1⊥平面BCC1B;
(II)求直线DA1与平面BCC1B1所成角的大小;
(III)求二面角A—DC1—C的大小。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三普通高考考生知识能力水平摸底考试数学理卷 题型:解答题
本小题共12分)
在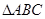 中,a,b,c分别为角A,B,C所对的边,向量
中,a,b,c分别为角A,B,C所对的边,向量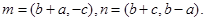 且
且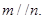
(I)求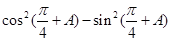 的值;
的值;
(II)若b=4,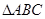 的面积为
的面积为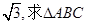 的周长。
的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com