
 已知函数
已知函数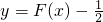
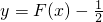 的零点是1和x0,若x0∈(n,n+1)(n∈N),求n的值;
的零点是1和x0,若x0∈(n,n+1)(n∈N),求n的值;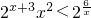 •(x2+3x-6)2.
•(x2+3x-6)2. (x>0)
(x>0) 与g(x)=log2x在(4,+∞)都是单调递增,
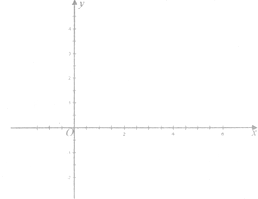
与g(x)=log2x在(4,+∞)都是单调递增, ,g(x)=log2x的图象有2个交点,其图象如图所示
,g(x)=log2x的图象有2个交点,其图象如图所示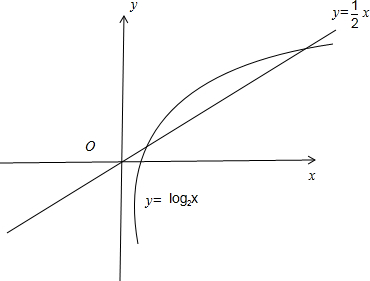
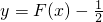 的零点是1可得
的零点是1可得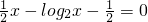 即x-1-2log2x=0的根为1和x0
即x-1-2log2x=0的根为1和x0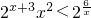 •(x2+3x-6)2.
•(x2+3x-6)2. +log2(x2+3x-6)2
+log2(x2+3x-6)2 <log2(x2+3x-6)2-log2x2
<log2(x2+3x-6)2-log2x2 (
(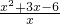 )<log2
)<log2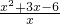
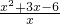 <4.
<4.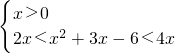 ①或
①或 ②
② (x>0)分类讨论:当0<x≤1时,当1<x<2时,比较f(x)和g(x)函数值的大小,进一步得出函数f(x)=
(x>0)分类讨论:当0<x≤1时,当1<x<2时,比较f(x)和g(x)函数值的大小,进一步得出函数f(x)= ,g(x)=log2x的图象有2个交点,再画出图象.
,g(x)=log2x的图象有2个交点,再画出图象.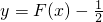 的零点是1可得
的零点是1可得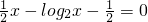 即x-1-2log2x=0的根为1和x0令G(x)=x-1-2log2x根据零点存在定理可知,x0∈(5,6)从而得出n=5;
即x-1-2log2x=0的根为1和x0令G(x)=x-1-2log2x根据零点存在定理可知,x0∈(5,6)从而得出n=5;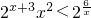 •(x2+3x-6)2.两边取以2为底的对数得:x+3+log2x2<
•(x2+3x-6)2.两边取以2为底的对数得:x+3+log2x2< +log2(x2+3x-6)2最后整理成
+log2(x2+3x-6)2最后整理成 (
(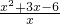 )<log2
)<log2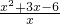 ,从而由(1)得出2<
,从而由(1)得出2<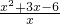 <4.解之即可.
<4.解之即可.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=|x-1|+|x+1|(x∈R)
已知函数f(x)=|x-1|+|x+1|(x∈R)查看答案和解析>>
科目:高中数学 来源:2014届浙江省高一下学期期中考试数学试卷(解析版) 题型:解答题
已知函数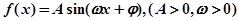 的图象在同一周期内最高点的坐标为
的图象在同一周期内最高点的坐标为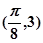 ,最低点的坐标为
,最低点的坐标为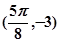 .
.
(1)求函数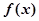 的解析式;
的解析式;
(2)求函数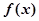 的单调递减区间.
的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com