
分析 (1)求出函数的表达式,利用函数的导数为0,得到极值点,然后求解极值.
(2)求出函数的解析式,利用换元法以及函数的导数,结合函数的单调性求解函数的最值即可.
解答 解:(1)因为函数f(x)=x2-x,g(x)=lnx,y=f(x)-g(x)
=x2-x-lnx,所以y′=2x-1-$\frac{1}{x}$=$\frac{(2x+1)(x-1)}{x}$
因为x≥0,所以当0<x<1时,y′<0;当x>1时,y′>0.
即函数y=f(x)-g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
故当x=1时,函数y有极小值0,无极大值.
(Ⅱ)函数y=f[xg(x)-2]=(xlnx)2-5(xlnx)+6,x∈[1,e],
令u=xlnx,当x∈[1,e]时,u′=lnx+1>0,所以u=xlnx在[1,e]上单调递增,
所以0≤u≤e,y=h(u)=u2-5u+6,
h(u)的图象的对称轴u=$\frac{5}{2}$.h(u)在[0,$\frac{5}{2}$]上单减,在($\frac{5}{2}$,e]上单增.
h(u)min=h($\frac{5}{2}$)=-$\frac{1}{4}$,又h(0)=6,h(e)=e2-5e+6,则h(u)max=6.
所以所求函数的值域为:[-$\frac{1}{4}$,6].
点评 本题考查函数的极值,函数的值域.导函数的单调性,构造法以及转化思想的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 18 | C. | -18 | D. | -$\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
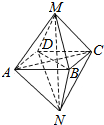 如图所示的几何体,关于其结构特征,下列说法不正确的是( )
如图所示的几何体,关于其结构特征,下列说法不正确的是( )| A. | 该几何体是由两个同底的四棱锥组成的几何体 | |
| B. | 该几何体有12条棱、6个顶点 | |
| C. | 该几何体有8个面,并且各面均为三角形 | |
| D. | 该几何体有9个面,其中一个面是四边形,其余均为三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com